日本ゼオライト学会　刊行物 Publication of Japan Zeolite Association

温室効果ガスの一種であるCO₂の排出量削減は，現代社会の大きな課題の一つである。また，近年ではカーボンニュートラルの実現に向けてCO₂の回収，再利用への関心が高まりつつあり，それに伴い，多孔性材料を用いたCO₂の分離に関する研究が注目されている。具体的には，ゼオライトや金属–有機構造体（Metal–Organic Framework; MOF，もしくはPorous Coordination Polymer; PCP）をはじめとした様々な多孔性材料を対象として，高いCO₂吸着能を持つ構造の開発が行われ，そのガス吸着特性に応じて圧力スイング法やガス透過法など様々な手法によるCO₂分離への応用が検討されている。

こうした材料開発～応用の研究プロセスにおいては，CO₂の吸着状態の解析を通じて，材料が高い（もしくは低い）CO₂吸着・分離能を示すメカニズムを明らかにし，その結果を材料設計へとフィードバックしたり，その材料を利用すべき環境や条件を把握したりすることが重要となる。材料中のCO₂吸着状態を解析する主な手法としては，X線回折法（X-ray diffraction; XRD）および中性子回折法が挙げられる。これらの手法は吸着したCO₂も含めた結晶構造を明らかにできるため，材料中の吸着サイトやCO₂の吸着状態を解析する上で有効である^1–5)。加えて，赤外分光法や計算科学手法などを用いた解析も，時にX線・中性子回折と組み合わせつつ行われている^6–10)。また拡散係数の測定には，中性子準弾性散乱法などが用いられている^11–14)。そして，CO₂の吸着・拡散挙動を調べるにあたっては，分子運動の解析を得意とする固体核磁気共鳴（Nuclear Magnetic Resonance; NMR）分光法が強力なツールとなる^{15, 16)}。X線・中性子回折法が静的・平均的なCO₂の吸着状態を明らかにするのに対し，固体NMRは，動的な吸着状態を詳細に観測できることが大きな特徴である。しかしながら，固体NMRがCO₂吸着状態の有効な解析手法であることは，あまり一般に認知されていないのが現状であろう。そこで本稿では，固体¹³C NMRによる材料の細孔中に吸着したCO₂のダイナミクス解析について，その原理と方法について解説するとともに，盛んに研究される多孔性材料の一つであるMOFを対象とした実際の研究例を紹介する。

細孔内におけるCO₂の分子運動は，主に①吸着サイトにおけるローカルな運動，②細孔内の拡散運動，の二つに分けられる。前者は具体的に，吸着サイト上における異方的な回転運動，および吸着サイト間のホッピング運動が存在する。これらの運動にはMOF–CO₂間やCO₂–CO₂間の相互作用，また細孔内の構造が反映され，吸着メカニズムに関する情報を我々に与える。一方，後者の細孔内拡散は吸着サイト間のホッピング運動が長距離にわたって生じたものと解釈することができる。その拡散係数はやはり吸着の強さや細孔径などと強く相関し，ガス透過分離法においては分離能を左右するパラメーターとなる。本章では，こうしたCO₂の運動を固体¹³C NMRによってどのように観測するのかについて説明する。

2.1 固体¹³C NMR測定の基礎

2.1.1 化学シフト相互作用

NMRは，静磁場中において原子核のスピンを観測する分光法である。核スピンは磁場中において，ゼーマン相互作用によってエネルギー状態の縮退が解けて分裂が生じ，その分裂幅に相当するエネルギーを信号として観測する。実際にはゼーマン相互作用以外にも，核スピンの周囲の環境によって大きさが変わる相互作用がいくつか存在し，これらがNMR信号に構造の情報を反映したピーク位置や線形を与える。固体¹³C NMRの場合，信号の位置や線形を主に決めるのは，核スピンとその周りの電子が作る磁場との相互作用である化学シフト相互作用である。この化学シフト相互作用は，等方的な成分と異方性を持った成分から構成される。前者は等方化学シフトと呼ばれ，信号の現れる位置を決定する。一方，後者は化学シフト異方性（Chemical Shift Anisotropy; CSA）と呼ばれ，NMRマグネットの静磁場に対する分子の向きによってその大きさが変化する。溶液NMRの場合は溶媒中のランダムな分子運動で後者が平均化され，前者によってピークの位置のみが与えられる。一方，固体の粉末試料では分子・結晶が磁場に対して様々な方向を向くため，その方向に応じた様々な位置に信号が現れる。結果として，スペクトルにはそれらをすべて合算した広幅な信号が観測され，これは粉末パターンと呼ばれる。

NMRの核スピン相互作用の大きさはテンソル量として表され，相互作用テンソルの主軸座標系においては，3×3の対角行列の対角成分に現れる三つの主値によってその大きさが決定づけられる。化学シフト相互作用では三つの主値（δ_XX, δ_YY, δ_ZZ）によって，等方化学シフト値δ_iso，CSAの大きさδ_aniso，および異方性の軸対称性を表す非対称性パラメーターηが|δ_ZZ－δ_iso|≥|δ_XX－δ_iso|≥|δ_YY－δ_iso|の条件の下，次のように定義される。

$$\begin{array}{}\text{(1)}& \begin{array}{c}{\delta }_{iso}＝\frac{1}{3}\left({\delta }_{XX}＋{\delta }_{YY}＋{\delta }_{ZZ}\right),{\delta }_{aniso}＝{\delta }_{ZZ}－{\delta }_{iso},\eta ＝\frac{{\delta }_{YY}-{\delta }_{XX}}{{\delta }_{aniso}}\end{array}\end{array}$$

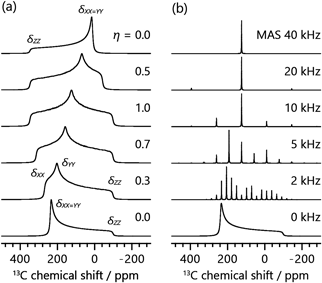
これらはスペクトルにおいて，図1aに示すような特徴的な線形を与える。¹³C核の場合，有機分子では主に結合する原子の種類によって¹³C核を取り巻く電子雲の形状や密度が変化するために，化学シフトテンソルの主値が変化する。例えば水素三つと結合したメチル基と酸素二つと結合したカルボキシ基では，等方化学シフト値およびCSAパラメーターはともに異なる値を示し，その結果スペクトル上において異なるピーク位置および粉末パターンの形状を与える¹⁷⁾。特にピーク位置については，官能基や化学種によってスペクトル上のどの範囲に信号が現れるかが大方決まっており，構造解析を行う上での重要な情報となっている。

図1. （a）化学シフト異方性（CSA）の影響を受けた粉末試料のNMR信号（粉末パターン）．δ_iso=125 ppmおよび|δ_aniso|=223 ppmとし，いくつかのηの値に対しスペクトルを計算した．化学シフトテンソルの主値（δ_XX, δ_YY, δ_ZZ）を対応する粉末パターンの角および肩の位置に示している．（b）マジック角回転（MAS）下におけるNMRスペクトル．δ_iso=125 ppm，δ_aniso=－223 ppm，η=0とし，MAS速度を変えながら計算した．

補足として，CSAパラメーターには上述のものとは異なる定義もあるため，文献などを参照する際は注意が必要である。また，NMRでは相互作用の大きさが周波数単位で表されるが，化学シフト相互作用の大きさは静磁場の強さに比例して変化する。そのため，数値を磁場強度に依存せずに取り扱えるよう，化学シフト相互作用の大きさは基準物質のピーク位置で決められた共鳴周波数で割って得られるppm単位の相対的な値によって示される。

2.1.2 マジック角回転法

固体粉末試料の広幅な信号に対し，異方性相互作用を平均化し信号を先鋭化する手法としては，試料管を静磁場に対して54.7°傾けた状態で高速回転するマジック角回転法（Magic Angle Spinning; MAS）が用いられる。MAS法は現代の固体高分解能NMRにおける重要なテクニックの一つであり，専用のMAS NMRプローブおよび回転試料管とともに一般に広く使用されている。図1bに示すように，CSAによる信号の線幅より十分に速いMAS速度を用いれば，異方性を消去し，溶液NMRのような等方化学シフトのみによる細い信号を得ることができる。MAS速度の周波数が線幅よりも小さい場合，等方化学シフトによるピークに加え，MAS周波数に応じた位置にスピニングサイドバンドと呼ばれるサブピークが現れ，結果としてスパイク状の信号を得る。このサイドバンド信号の強度比は，静止試料の粉末パターンの線形と同様，CSAの大きさに応じて変化する。したがって，サイドバンドパターンからCSAパラメーターを抽出することが可能である。

2.2 CO₂のローカル運動の測定・解析

2.2.1 化学シフト異方性による線形の解析

CO₂は常温常圧で気体であるため，その¹³C信号は，CSAがランダムな分子運動で平均化された等方化学シフトのみによるシャープなピークとなる。一方，195 K以下における固体状態ではCSAによる粉末パターンが観測され，そのパラメーターはδ_aniso=－223 ppm, η=0と報告されている¹⁸⁾。吸着状態においては，吸着サイトとの相互作用や細孔内の立体障害を受けて分子運動が異方的に制限され，¹³C信号は気体分子でありながらCSAの影響を受けた粉末パターンとなる。この線形を解析することにより，細孔中のCO₂の動的な吸着状態を明らかにすることができる。CO₂は吸着サイト上において一軸回転運動を行うことが知られ，運動速度を10⁶ Hz以上と仮定したとき，回転軸に対する傾きの角度θに応じて見かけのCSAの大きさδ′_anisoが次式のようにスケールされる。

$$\begin{array}{}\text{(2)}& \begin{array}{c}{{\delta }^{\prime }}_{aniso}＝\frac{1}{2}\left(3{\cos }^2\theta －1\right){\delta }_{aniso}^0\end{array}\end{array}$$

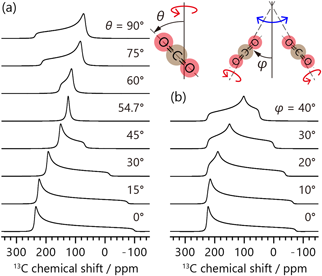
δ⁰_anisoは先述の固体のCO₂のCSA値である。室温付近およびより高温においては，運動速度は10⁶ Hz以上としてほぼ問題ないであろう。θの値に応じた粉末パターンの変化の様子を図2aに例示した。式（2）を用いることで，吸着したCO₂の粉末パターンの線形より得られるCSAの大きさδ′_anisoより，回転運動の傾きの角度θを明らかにできる。また2.1.2で述べたように，遅いMAS速度の下で現れるサイドバンドパターンからもδ′_aniso，そしてθを得ることが可能である。δ′_anisoを得るための線形解析は，測定データに対するピークフィッティングにより可能である。これには固体NMRスペクトルの解析に対応した専用のソフトウェアが必要であり，筆者はフリーソフトであるssNaKe¹⁹⁾を利用している。もしくは，スペクトルシミュレーションによる解析も可能である。この場合はδ′_anisoを得るのではなく，θの値を変えながらスペクトルを計算し，実験結果を再現するθを直接探す作業になる。図2aは実際に固体CO₂のCSA値（－223 ppm）を用いて様々なθにおける回転運動下のスペクトルを計算することで得ている。これもやはり専用のソフトウェアが必要であり，フリーソフトであればMATLAB上で動作するEXPRESS²⁰⁾が使用可能である。

図2. （a）様々な傾き角θにて一軸回転運動を行うCO₂，および（b）回転軸の向きの変化を伴うθ=15°の一軸回転運動を行うCO₂の¹³C CSAによる粉末パターン．δ_iso=125 ppm，δ_aniso=－223 ppm，η=0とし，また後者は回転軸の向きφで定義される2つのサイト間のホッピングを想定してスペクトルを計算した．

先述の通り，CO₂は回転運動に加えて，吸着サイト間をホッピング運動している。このホッピングに伴って結晶構造中における回転運動の軸の向きが変化する場合，回転軸に対する傾きθに加えて，回転軸の角度変化の影響も粉末パターンに現れる。その結果，信号は非対称性パラメーターη≠0の粉末パターンのような線形となる。一例を図2bに示した。このような場合，フィッティングで得られる見かけのCSAパラメーターからθおよび回転軸の角度変化の大きさを求めることはできず，分子運動を考慮したスペクトルシミュレーションによる解析が必要となる。

なお，本稿では化学シフト相互作用のみによって線形が決まる場合を取り扱うが，吸着サイト付近に常磁性を持つ原子がある場合，その電子スピンと¹³C核との相互作用によっても信号の位置や線形が変化するため，解析が煩雑になる。そのためMOFでは，Zn²⁺など反磁性金属イオンからなる構造に対してNMR測定・解析が行われる場合が多い。

2.2.2 等方化学シフト値を用いた解析

細孔表面に物理吸着したCO₂は，吸着サイトとの静電的相互作用によって¹³C信号の等方化学シフト値に変化が生じ，そのピーク位置は気体状態と比べてわずかに低周波数（低ppm）側にシフトすることが知られている。気体のピーク位置が125 ppm程度である場合，吸着したCO₂の等方化学シフトによるピークの観測範囲は，おおよそ122–125 ppmである。等方化学シフト値は，静止試料の広幅な粉末パターンを解析するより，MASで先鋭化した信号から直接取得する方が高精度に得られやすい。ピークの位置は吸着サイトとの相互作用の強さにある程度依存すると考えられるが，MOFにおいては両者の関係性を系統的に調べ，ピーク位置から相互作用の強さを議論した報告例はなく，等方化学シフトの値そのものから吸着状態を評価することは現状難しい。あるいは，量子化学計算による化学シフトの予測と組み合わせることが有効かもしれない。なお，溶液¹³C NMRでは一般に標準物質であるテトラメチルシランの信号をスペクトルの0 ppmと定めるが，固体¹³C NMRではアダマンタンやグリシンなどの2次標準物質を用いて化学シフト値を校正することが多い。どの2次標準物質のどのピークをテトラメチルシランに対して何ppmと設定するかは文献によって少しずつ差があるため，化学シフト値の校正や文献との比較を行う際は注意を要する。また試料中に常磁性原子が存在する場合，先述の常磁性相互作用によって吸着したCO₂のピークが気体より高周波数側にシフトしうるため，こちらも注意が必要である^{21, 22)}。

細孔中に異なる複数の吸着サイトが存在し，CO₂がそれらの間をNMRの信号観測の時間スケール（¹³C MAS NMRの場合ms程度）より十分速く行き来している場合，ピークはそれぞれの吸着サイトに対応した位置ではなく，それらを平均化した位置に観測される。この平均的なピーク位置は，各吸着サイトへの吸着量の比で重みづけされる。そのため，吸着等温線を参考にいくつかの圧力で測定を行うことで，ピーク位置の圧力依存性より複数ある吸着サイトがどう埋まっていくのかを解析することができる。

2.2.3 スピン–格子緩和時間を用いた解析

試料を静磁場中に入れた直後やNMR信号の観測直後から磁化，つまりNMR信号が熱平衡状態へと向かう過程はスピン–格子緩和と呼ばれる。磁化Mが熱平衡状態M₀に向かって回復する様子は，時定数T₁を用いて

$$\begin{array}{}\text{(3)}& \begin{array}{c}M(t)＝M_0\left\{1－\exp \left(－\frac{t}{T_1}\right)\right\}\end{array}\end{array}$$

と記述される。実験的には主に飽和回復法や反転回復法によって測定され，これらは現代のNMR分光計には標準的に備わっている測定法である。NMRの緩和は核スピン相互作用によって核が感じる局所磁場が分子運動で揺らぐことによって生じ，局所磁場の揺らぎの速度，すなわち運動の速度に応じて緩和時間は変化する。そのため，試料温度を変化させ分子運動の速度を変えながら緩和時間測定を行い，得られたT₁の温度依存性を解析することでその運動性を調べることができる。CO₂の¹³C核では化学シフト相互作用が緩和に寄与し，緩和速度1/T₁^CSAはBPP式と呼ばれる次の式で表される²³⁾。

$$\begin{array}{}\text{(4)}& \begin{array}{c}\frac{1}{T_1^{CSA}}＝C\frac{{\tau }_c}{1＋{\omega }_{0C}^2{\tau }_c^2}\end{array}\end{array}$$

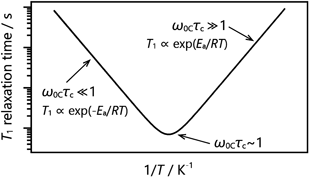
CはCSAの大きさと運動モードに依存した定数，ω_0Cは¹³C核の共鳴周波数であり使用するNMR装置の磁場強度による。τ_cは運動の相関時間，つまり運動速度の逆数であり，大抵アレニウス式τ_c=τ₀ exp(E_a/RT)で記述される。式（4）は温度の逆数に対して図3のような曲線となり，実験で得たT₁に対してC，τ₀, E_aを変数としてフィッティングを行い解析する。これより，運動の活性化エネルギーE_aと運動速度1/τ_cが求められる。詳細は説明しないが，Cから運動モードを解析することも可能である。なお，T₁の値はω_0Cτ_c ～1において図3のT₁曲線を特徴づける極小値を取るが，運動の速度や実験条件によっては極小値を観測できないことがある。この場合，式（4）を解析に使うことは難しいが，運動の速度1/τ_cが共鳴周波数ω_0Cより十分遅い領域では，ω_0Cτ_c≫1より式（4）を近似した

$$\begin{array}{}\text{(5)}& \begin{array}{c}\frac{1}{T_1^{CSA}}~\frac{C}{{\omega }_{0C}^2}{\tau }_c^{－1}\end{array}\end{array}$$

逆に運動が共鳴周波数ω_0Cより十分速い領域では，ω_0Cτ_c≪1より

$$\begin{array}{}\text{(6)}& \begin{array}{c}\frac{1}{T_1^{CSA}}~C{\tau }_C\end{array}\end{array}$$

によって解析を行うことができる。ただしこれらの式によるフィッティングでは，Cとτ₀はそれらの積としてしか得られず，したがって明らかになるのはE_aのみである。

図3. スピン–格子緩和時間T₁の温度依存性のlogプロット．曲線の極小値より低温側および高温側は単一の指数関数に近似でき，その傾きは活性化エネルギーE_aに相当する．

MOFのように細孔中に水素原子が多く存在する場合，その¹H核とCO₂の¹³C核との間に，大きさが核間距離に依存する双極子相互作用が働く。化学シフト相互作用と同様に双極子相互作用も緩和に影響し，その緩和速度1/T₁^dipは

$$\begin{array}{}\text{(7)}& \begin{array}{c}\frac{1}{T_1^{dip}}＝D\left\{\frac{{\tau }_c}{1＋{\left({\omega }_{0H}－{\omega }_{0C}\right)}^2{\tau }_c^2}＋\frac{3{\tau }_c}{1＋{\omega }_{0C}^2{\tau }_c^2}＋\frac{6{\tau }_c}{1＋{\left({\omega }_{0H}＋{\omega }_{0C}\right)}^2{\tau }_c^2}\right\}\end{array}\end{array}$$

と与えられる²³⁾。Dは双極子相互作用の大きさとCO₂の運動性に依存し，ω_0Hは¹H核の共鳴周波数である。またCO₂の¹³C核のT₁は，これら二つの相互作用による緩和速度の和(1/T₁^CSA)+(1/T₁^dip)で与えられる。なお，T₁の極小が観測できない場合は，双極子相互作用の寄与の有無にかかわらず，やはり式（5, 6）の近似式で解析することになる。

2.3 CO₂の拡散運動の測定・解析

2.3.1 拡散NMR法

CO₂を含む様々なガス分子やイオン，溶液中の分子などの拡散係数が拡散NMR法によって測定されている。測定は，NMRマグネットの静磁場に磁場勾配を生じさせて行われる。スペクトルにおけるNMR信号の位置を主に決めるゼーマン相互作用および化学シフト相互作用の大きさは，磁場強度に比例する。そのため，磁場勾配があると試料位置によって磁場強度が変化し，それに応じて信号の位置に違いが生じる。試料中で分子やイオンが動き回る場合，移動距離に応じて信号の位置が変化するので，これを利用することで拡散係数を解析することができる。非常に強力な測定法だが，磁場勾配をかけられる専用のNMRプローブおよび磁場勾配パルスを用いた特殊な測定シークエンスが必要となる。測定・解析法の詳しい説明はここでは割愛するが，詳細を知りたい場合は例えば「竹腰清乃理著：磁気共鳴–NMR―核スピンの分光学―」の10.6節に測定法についてコンパクトにわかりやすく書かれている。また，筑波大学の早水先生がhttps://diffusion-nmr.jp/にて主にLiイオンの拡散NMR測定に関する詳細な解説を公開されており，こちらも非常に参考になるであろう。ちなみにMOF細孔中におけるCO₂の拡散係数は，細孔の構造に依存するものの，一般的には10⁻⁸–10⁻¹⁰ m²/s程度と拡散NMR法により測定されている^24–29)。

2.3.2 交差分極法

交差分極法（Cross Polarization; CP）は，核スピン間の双極子相互作用を利用してある核から別の核に磁化を移動し観測する方法である。固体の有機物の¹³C測定においては，周囲に多く存在し測定感度のよい¹H核から磁化を移すことで，¹³C核の信号強度を増幅し，測定効率を大幅に向上できる。そのため，MAS法とともに現代の固体NMRの重要なテクニックの一つとなっている。緩和の項で説明したように，MOF細孔中ではCO₂の¹³C核が周囲の¹H核と双極子相互作用を形成する。しかしながら，双極子相互作用の大きさは核間距離の3乗に反比例し，吸着したCO₂は拡散によって周囲の¹Hと距離が離れて双極子相互作用が弱まってしまう。そのため，基本的にはCP法で信号を検出することはできない。筆者の経験的に，先述の一般的な拡散係数を示すMOF中のCO₂に対しては，室温付近およびそれ以上の温度下ではCP法が効かない。まれに，細孔内部の立体障害や吸着サイトとの強い相互作用などによってCO₂の拡散速度が遅く，CP法でCO₂の¹³C信号を観測できる場合がある^30–33)。拡散速度を調べる測定法ではないため，拡散NMRのように拡散係数を求めることはできないが，拡散係数が一般的な値程度かそれより小さいかの判断など，定性的な解析は可能である。

2.4 同位体核種濃縮CO₂ガスの使用

¹³C核の天然存在比は1%程度であり，残りの99%はすべてNMRで観測できない¹²C核である。そのため，特にCO₂の吸着量が少ない圧力条件下や，信号が広幅な静止状態では，信号を観測するためのスペクトルの積算に数時間から場合によっては1日以上を要することが予想される。信号の感度向上のため，費用はかかるが¹³C同位体濃縮したCO₂ガスを利用することが望ましい。なお，¹⁷O同位体濃縮ガスを用いれば固体¹⁷O NMRによる測定・解析も可能であり，そのような例も報告されている³⁴⁾。本稿では解説しないが，¹⁷O核は四極子相互作用も持つため，化学シフト相互作用と組み合わせることでより詳細な運動状態の解析が可能となる。

2.5 CO₂雰囲気下測定のための試料管準備

CO₂を吸着した試料の固体NMR測定は，試料管内に試料とCO₂ガスを入れた状態で行われる。一般的な固体NMRの回転試料管は気密性に乏しいため，測定には何らかの工夫が必要となる。気密性を高めた特殊な試料管のキャップも売られており，例えばCO₂を充填したグローブボックス中などで試料管に取り付けることで，試料管内に試料とCO₂を閉じ込めることができる。しかしこの場合，ガスの使用量が多いため同位体濃縮ガスは使用できず，また圧力も大気圧に限られる。そこで本節では，CO₂雰囲気下で測定を行うための試料管準備の方法を紹介する。

2.5.1 ガラス管の使用

CO₂を含む特殊雰囲気下における固体NMR測定で一般的に行われるのが，試料を詰め任意の圧力のガスを充填したガラス管をガスバーナーで焼き切って封じる方法である。MOFにおいては，吸着したCO₂の固体NMR測定のほとんどがこの方法で行われている。ガラス管の封管には慣れが必要だが，静止試料の測定はこれで問題なく行うことができる。ただし，MASを行いたい場合，封管したガラス管が回転試料管に入るため，回転による遠心力でガラス管が破損するリスクや，ガラス管の形状によっては回転が不安定になり試料管が破損するリスクがある。

NMR装置外部でガスボンベに接続した単結晶サファイア製の試料管をNMRプローブ中に設置することで，測定環境下で試料に様々なガス圧を印加するin situ測定を行った例が報告されている^{35, 36)}。このような装置は筆者が知る限り市販されておらず，自作が必要となるが，一つの試料に対して連続的にガス圧を変化できる点は大きなメリットである。先行研究においてはCO₂を大気圧以下～約10気圧，Xeでは20気圧近くまで変化させ，固体¹³Cおよび¹²⁹Xe NMR測定を行っている。ガラス管で同様の装置を作製することで，サファイアと比べて耐圧性は低下するものの，様々なガス圧力下で測定を行う場合には有効に運用できると期待される。ガラス管で作製した装置でex situ測定を行った例も報告されている³⁷⁾。

2.5.2 特殊な回転試料管の作製

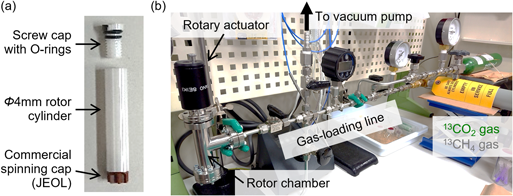
市販の回転試料管の規格を基に，Oリングの付いたスクリュー式キャップを備えた高気密性の回転試料管を設計した報告がある³⁸⁾。筆者らはこの報告を参考に，図4に示すような気密性回転試料管を設計・作製し，更に任意の圧力のガス雰囲気下で試料管のキャップを開閉できるガス配管を開発することで，CO₂雰囲気下におけるMOFの¹³C MAS NMR測定を行っている^{33, 39)}。これまでに10気圧程度までは漏れなくCO₂を封入できており，ガラス管と比べてMASによる高感度・高分解能測定が容易である点や，1度試料管に詰めた試料に対し様々なガス圧を印加できる点などから，利便性の高い手法と言える。

図4. （a）ガス雰囲気下MAS NMR測定用のジルコニア製回転試料管．市販のJEOL 4 mm回転試料管の形状を基に筆者らが設計した．ネジ式の上部キャップに取り付けたOリングによって試料管内に大気圧以上のガスを封じることができる．試料管へのガスの導入は（b）に示す配管を用いて行う．回転導入器を用いることで，任意の圧力のガス雰囲気下にて試料管のふたを開閉できる．

MOFは，金属イオンと配位子の配位結合から形成される多次元的な骨格を持った多孔性材料である。用いる金属種と配位子の組み合わせによって多彩な構造が合成でき，また配位子への置換基の導入などによって細孔中に立体障害や新たな吸着サイトを導入可能といった特徴を持つ。こうした構造の設計性の高さから，これまで数万種類のMOFが作製され，その吸着特性が盛んに研究されている。固体NMRはMOFの局所構造やゲスト分子の吸着状態の解析にしばしば用いられてきたが，吸着したCO₂のダイナミクスが固体¹³C NMRによって解析されるようになったのはここ10年ほどであり，報告されている文献も筆者が知る限り30報程度とそれほど多くはない。しかしながら，その多くが固体NMRによる解析特有のCO₂の吸着状態の情報を得ることに成功している。以下では，代表的ないくつかの論文について取り上げ，解説する。

3.1 CO₂のローカル運動

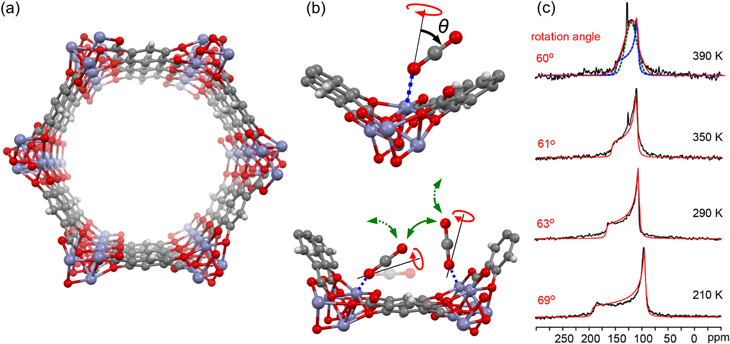
固体¹³C NMRによってMOFに吸着したCO₂の運動性を解析する試みは，2012年にU. C. BerkeleyのReimerグループにより初めて行われた⁴⁰⁾。用いられたのはMOF-74と呼ばれるハニカム型構造の1次元細孔を有するMOF（図5a）であり，化学的安定性の高さなどから盛んに研究されている。ReimerらはMOF-74中のCO₂に対し，¹³C CSAによる粉末パターンを解析することで，吸着状態のCO₂が一軸回転運動を行うことを初めて提唱した。回転運動の傾きの角度θは～60–70°程度の範囲であり，温度が上昇するとθが小さくなることや，また吸着量によってもθが変化することを示した（図5b，c）。また，¹³C T₁緩和時間の温度変化の解析よりE_aを求め，吸着量増加によりE_aが小さくなることからCO₂と吸着サイトの相互作用が弱まっている可能性を指摘した。このように，固体NMRでCO₂の吸着状態を詳細に解析できることを示した重要な研究である。彼らはその1年後，モンテカルロ法による細孔中のCO₂の自由エネルギーの計算より，MOF-74中のCO₂は一軸回転運動でなく揺動運動と吸着サイト間のホッピング運動を行っている可能性を提案し，そのような2種類の運動の組み合わせでもCSAの粉末パターンを再現しうることを報告している⁴¹⁾。その翌年にはThe University of Western OntarioのHuangらによって固体¹⁷O NMR測定が行われ，¹⁷O核のCSAと四極子相互作用が合わさった線形の解析により，θ～20–30°程度の一軸回転運動と吸着サイト間のホッピング運動（図5b）が起きていると提案された³⁴⁾。

図5. （a）ハニカム型構造を有するMOF-74の結晶構造．6角形の頂点に位置する部位が主な吸着サイトとして知られる．（b）MOF-74に吸着したCO₂の運動モデル．上が一軸回転運動，下が一軸回転と吸着サイト間ホッピングの複合運動．（c）ReimerらによるMOF-74中のCO₂が一軸回転運動を行っているとした場合の¹³C粉末パターンの解析結果⁴⁰⁾．[Adopted with permission from ref 40. Copyright 2012 American Chemical Society.]

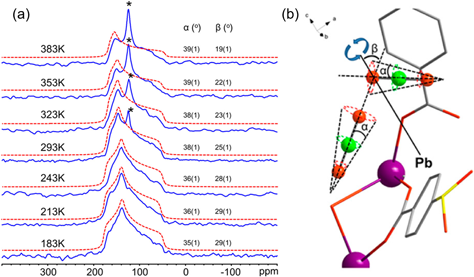
HuangグループはMOF-74以外にも，様々なMOF中に吸着したCO₂のダイナミクス解析に取り組んでいる。彼らは¹³C CSAによる粉末パターンを利用したローカル運動の解析に加え，¹³C CP測定やXRD，計算科学手法などによる静的な吸着構造の解析も行うことで，CO₂の吸着状態を効果的に解析している。例えば，CdSDBおよびPbSDBと呼ばれるCd²⁺およびPb²⁺からなる構造のMOFに対し，単結晶XRDと固体¹³C NMRを組み合わせた解析を行っている⁴²⁾。CO₂吸着下での単結晶構造解析によってMOF中のCO₂吸着位置を特定し，また¹³C粉末パターンを解析することで，CO₂が吸着サイト上でどのように運動し，また吸着サイト間をどのようにホッピングするのかを明らかにした（図6）。固体NMRは局所的な静的・動的構造の解析を得意とする一方，結晶構造のような全体構造を把握することは難しく，またXRDは逆の性質を持つため，これら二つの手法を相補的に組み合わせることは非常に有効と言える。α-Mg formateと呼ばれるMg²⁺とギ酸イオンからなるMOF中のCO₂に対しては，¹³C粉末パターンによる一軸回転運動およびホッピング運動の解析に加え，分子動力学計算によって細孔中のCO₂の位置を解析している⁴³⁾。計算で得られたCO₂の位置の分布はNMRから得られた分子運動の様子とよく一致しており，計算結果の妥当性を実験的に示しつつ，細孔内でのCO₂の動きや吸着部位を可視化することに成功している。

図6. （a）PbSDB中に吸着したCO₂の¹³C粉末パターン（実線）および一軸回転運動と二つの吸着サイト間のホッピング運動を仮定したシミュレーション線形（破線）．（b）単結晶XRDより得られた，吸着したCO₂を含むPbSDBの局所構造．固体¹³C NMRより明らかにされたCO₂の運動の様子も示されている．[Adopted with permission from ref 42. Copyright 2016 American Chemical Society.]

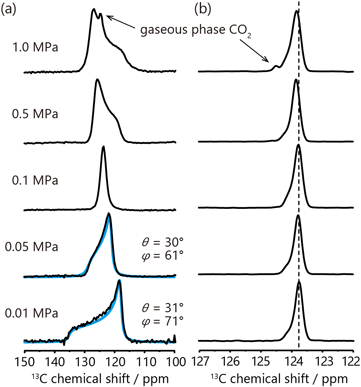
上記の例はすべて静止状態の試料の固体NMR測定により行われているが，MAS法を用いた解析の例も紹介する。UTSA-16と呼ばれるMOFに吸着したCO₂に対し，MASによりCSAが平均化され先鋭化した¹³C信号のピーク位置の温度変化から，温度に応じた吸着部位の変化が解析されている²²⁾。ピーク位置の変化の幅は1 ppm程度であるが，MASを行わない場合はCSAとMOF中の常磁性Co²⁺イオンの影響で粉末パターンは300 ppmに及ぶ線幅を示しており，このような等方化学シフト値の小さな変化が検出できたのはMAS法を用いたためと言える。筆者らは気密性の回転試料管を作製し，先述のMOF-74に対し0.01–1 MPaのCO₂圧力下で¹³C MAS NMR測定を行った³⁹⁾。MASで先鋭化したCO₂の¹³C信号からは圧力上昇に伴う0.1 ppm程度のピークシフトが観測されている（図7）。MOF-74中においてCO₂はガス圧の上昇に伴い，低圧時に吸着する第1吸着サイトとは異なる第2吸着サイトにも吸着し，それらサイト間のホッピングによる交換の様子がピークシフトとして現れていると解釈できる⁴⁴⁾。10–20 ppm程度の線幅を示す静止状態の粉末パターンの解析では，0.1 ppm程度のピークシフトはノイズによる誤差に埋もれてしまう可能性があり，やはり等方化学シフト値の解析におけるMAS法の有効性がうかがえる。

図7. MOF-74中に吸着したCO₂の固体¹³C NMRスペクトル．測定は0.01–1 MPaの圧力下にて，（a）静止状態および（b）MAS下の試料に対し行われた．0.01および0.05 MPaの粉末パターンに対し，図5bの一軸回転+サイト間ホッピング運動を用いて行った線形シミュレーションの結果も示している．

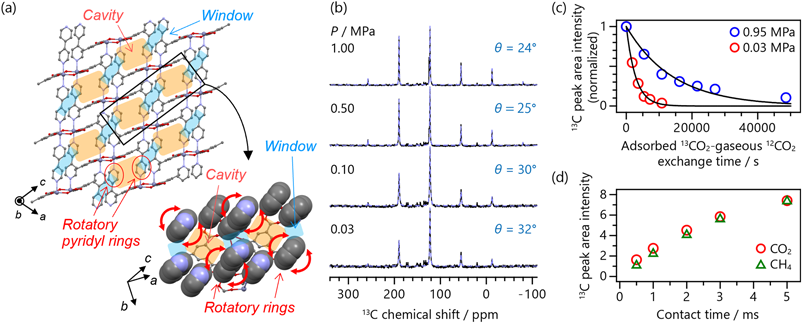
CO₂の一軸回転運動の傾きおよびホッピング運動による角度変化が小さいとき，粉末パターンは線幅が200–300 ppmに及ぶような非常に広幅な信号を示す。このような場合は静止状態で測定するより，数kHz程度でMASを行いスピニングサイドバンドによって信号をスパイク上にすることで，測定感度を大きく向上しつつCSA解析を行える。筆者らは，CID-Meと呼ばれるMOF（図8a）の狭い1次元細孔中に吸着したCO₂に対し，¹³C MAS NMR測定を行いその運動性を解析した³³⁾。細孔中の吸着部位であるキャビティ部にCO₂が1分子吸着する0.03 MPaから2分子吸着する1 MPaまで圧力を変化させて測定し，サイドバンドパターンに対するフィッティングでCSA値を取得し式（2）によって回転の傾きθを求めた（図8b）。その結果，0.03 MPaではθ=32°，1 MPaではθ=24°と吸着量の増加に伴うθの減少が確認された。これは，CO₂が狭い細孔内にて配位子や別のCO₂による立体障害を受け，運動が制限されていることを示している。CID-Meは細孔のウィンドウ部（図8a参照）において配位子の一部が回転運動を有しており，この回転の際に細孔径が2.5 Åから3.4 Å程度まで動的に拡大する特徴を持つ。筆者らは固体²H NMR測定により，高圧下ではキャビティ部に2分子吸着したCO₂が立体障害となり，配位子の運動性も制限される様子を観測した。これらの知見を基に，配位子の運動性の低下による細孔径の拡大の抑制がCO₂の細孔内拡散に影響を及ぼすことを見出しており，その詳細は次節にて紹介する。

図8. （a）CID-Meの結晶構造および細孔部分を拡大した局所構造．1次元細孔のキャビティ部およびウィンドウ部をハイライトして示している．（b）CID-Me中に吸着したCO₂の¹³C MAS NMRスペクトル（実線）およびサイドバンドパターンに対するフィッティング結果（破線）．解析より得られた回転の傾き角θも示した．（c）吸着¹³CO₂–気体¹²CO₂交換実験により得られた，吸着したCO₂の¹³C信号強度の変化．0.03および0.95 MPaの圧力下で実験を行い，指数関数を用いたフィッティング（実線）よりそれぞれの圧力での交換速度を3.5×10⁻⁴および7.0×10⁻⁵ s⁻¹と得た．（d）CID-Me中に吸着したCO₂（0.03 MPa）およびCH₄（0.10 MPa）の¹³C CP信号のコンタクトタイム依存性．

3.2 CO₂の細孔内拡散

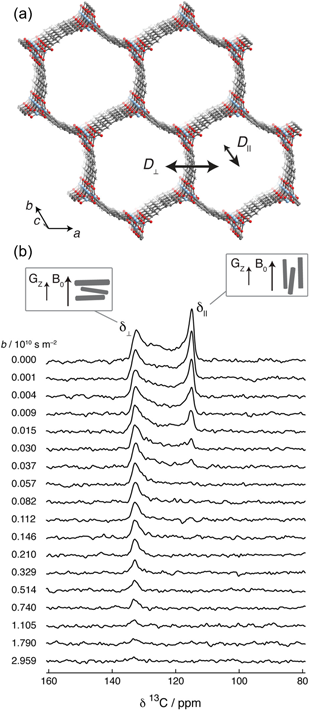
CO₂の拡散の解析では，多くの場合拡散NMR法が用いられている。MOF細孔中におけるCO₂に関しては，先述の通り，10⁻⁸–10⁻¹⁰ m²/s程度の拡散係数が拡散NMR測定により観測されている。通常の測定では単一の拡散係数が得られるのみにとどまるが，中には粉末パターンを利用することで，細孔構造に依存した拡散速度の異方性を解析した報告もある。2.1節で述べたように，固体試料は異方性相互作用のため，NMRの静磁場に対する結晶や分子の向きによってピーク位置が変化し，その足し合わせが粉末パターンである。吸着したCO₂の場合も同様に，ホストである結晶の磁場に対する向きとともにCO₂の向きが変わり，CSAにより¹³Cピークの位置が変化する。ここで，例えば結晶のa軸方向とbc軸方向で細孔径が異なるような異方的な細孔構造の場合，結晶の向きとともに異方的な細孔の向きも変化するため，CO₂の¹³C粉末パターンは磁場に対する細孔の向きを反映したものとなる。これに対して拡散NMR測定を行い，磁場勾配による粉末パターンの変化を解析することで，拡散係数の細孔方向依存性を測定した例がいくつか報告されている^{27–29, 37)}。ここでは一例として，先述の1次元細孔を持つMOF-74の同形構造体（図9a）に対する，Reimerらによる測定結果を紹介する^{28, 37)}。実験では1次元細孔方向に長い針状の結晶が使用され，図9bに示すように，吸着したCO₂の粉末パターンの低周波数側および高周波数側のエッジが，それぞれ静磁場B₀方向に対し結晶が平行および垂直に向く場合と対応する。磁場勾配パルスG_zをB₀と平行方向に印加しながら¹³C拡散NMR測定を行ったところ，パルス強度の増加に伴い粉末パターンの低周波数側がより速く強度が減衰する様子が観測された。このことは，1次元細孔方向の拡散の方が，細孔と垂直方向の拡散よりも速いことを示している。彼らはスペクトルシミュレーションによる解析より，1次元細孔方向の拡散係数（D_//）を6.5×10⁻⁹ m² s⁻¹，細孔と垂直方向（D_⊥）を3.9×10⁻¹¹ m² s⁻¹と得ている。1次元細孔にも関わらず細孔と垂直方向にCO₂が拡散できるのは，欠陥により細孔壁に穴が空いているためとされる。

図9. （a）MOF-74の同形構造体であるZn₂（dobpdc）の結晶構造．1次元細孔中におけるCO₂の拡散の方向に対応して拡散係数D_//およびD_⊥が図のように定義されている．（b）Zn₂（dobpdc）中のCO₂の¹³C拡散NMRスペクトル．静磁場B₀と平行方向に印加した磁場勾配パルスG_zの強度を上げながら測定された．B₀に対するMOFの結晶の向きと粉末パターンのエッジとの対応が示されている．[Adopted with permission from ref 28. Copyright 2018 American Chemical Society.]

筆者らは拡散NMR以外の手法で拡散速度を見積もる試みを行っており，これについても紹介する。3.1節で述べたように，筆者らはCID-Meと呼ばれるMOFの1次元細孔中にて，CO₂の吸着に伴い配位子の運動性が低下する様子を観測した。このCID-Meの細孔径は配位子の回転の際に拡大する性質を持ち，したがって高圧下にて回転速度が低下することで細孔径拡大が抑制され，CO₂の拡散が遅くなると予想される。これを実証するため，初めにMOFに¹³C同位体濃縮CO₂（¹³C 99%）を吸着させ，その後MOFを通常のCO₂（¹²C 99%）下に置くことで細孔内の¹³CO₂と¹²CO₂を交換し，その速度を¹³C MAS NMRでモニターするという実験を行った。細孔内に吸着したCO₂が細孔外の気体のCO₂と入れ替わる過程では細孔内の拡散を経ることになるため，交換速度には拡散速度が反映されると期待される。圧力条件を細孔キャビティ部にCO₂が一つ吸着する0.03 MPaおよび二つ吸着する0.95 MPaと設定し，図4に示したスクリューキャップ式の気密回転試料管および専用に設計した配管を用いることで各圧力下において¹³CO₂を吸着したMOFを¹²CO₂に晒し，¹³C信号の経時変化を観測した。その結果，図8cに示すように吸着した¹³CO₂の信号強度が¹²CO₂との交換で徐々に減衰していく様子が確認された。指数関数によるフィッティングより交換速度は0.03 MPaでは3.5×10⁻⁴ s⁻¹，0.95 MPaでは7.0×10⁻⁵ s⁻¹と得られ，配位子の回転速度が低下する高圧下にてCO₂の細孔内拡散速度も低下することが示された。なお，実験に用いたMOFの結晶サイズ（～10–50 µm）より拡散係数を概算すると10⁻¹³–10⁻¹⁵ m² s⁻¹となり，一般的なMOF中のCO₂の拡散よりもだいぶ遅いことがわかる。これは狭い細孔中における回転する配位子の立体障害の影響であり，このような細孔構造だからこそ配位子の回転速度がCO₂の拡散に影響を及ぼしたと考えられる。

このCID-Meの研究において，筆者らはCP法を用いた拡散速度の解析も行った。CID-Meに吸着したCO₂は遅い拡散によりCP法で¹³C信号が観測できる。CPにおける磁化移動の速度は，核間距離に依存した双極子相互作用の大きさによる。そのため，磁化を移すCPパルスの照射時間（コンタクトタイム）に依存してどのように磁化が増幅されるかを調べることで，核間距離の情報が解析できる。研究ではCO₂と比較的分子サイズが近く，また一般にCO₂より吸着が弱いCH₄について，CID-Meに吸着した場合CP法で¹³C信号が観測できることを確認したため，その信号強度のコンタクトタイム依存性を測定し，CO₂との比較を行った。その結果，図8dに示すように両分子ともほぼ同様のコンタクトタイム依存性を示した。CH₄は吸着状態でも分子全体が回転運動をしており⁴⁵⁾，これにより分子内の¹H–¹³C双極子相互作用が平均化されCPに寄与しないため，CO₂同様に配位子の¹Hからの磁化移動で信号が観測されている。したがってこの結果は，CO₂およびCH₄の¹³C核と配位子の¹H核との平均核間距離が同程度，すなわち同じような速度で拡散していることを示している。一般に吸着の弱いCH₄の方が細孔内を拡散しやすいと予想されるが，狭い細孔内では吸着の強さよりも立体障害が拡散速度に効くと考えられる。このような状況下で立体障害となる配位子の回転速度を制御できれば，ガスの拡散速度は分子サイズ選択的にコントロール可能であることを本研究は提案する。

本稿では，固体¹³C NMRによって吸着したCO₂の分子運動がどのように観測されるのか，その理論的背景とMOFを対象とした実際の解析例について解説した。固体NMRでは細孔内におけるCO₂のローカルな運動，具体的には吸着サイト上での回転運動や吸着サイト間のホッピング運動を，運動の角度や速度，活性化エネルギーまで解析可能である。そのため，細孔中にCO₂がどのように取り込まれているのかを詳細に明らかにすることができる。また，細孔内における拡散速度の評価も可能であり，これは特にガス透過分離において分離能を左右する重要なパラメーターとなる。加えて，固体NMRにXRDや計算科学手法による吸着状態の解析を組み合わせることも有効な方法である。こうした解析法はMOFに限らず，ゼオライトなど他の多孔性材料に対しても適用可能であろう。またCO₂以外のガス種に対しても，やはり同じように解析が可能であり，MOFに吸着したH₂やCH₄などを対象とした研究が報告されている¹⁶⁾。ここまで紹介したものはすべて単一のガス種の吸着状態を調べたものだが，一方で実際のガス分離の対象となる混合ガスについては，MOFにおいては筆者が知る限り固体NMRで吸着状態のダイナミクスを調べた例は報告されていない。混合ガス下における吸着状態を調べることで，ガス分離等のメカニズムを分子レベルで解析可能であろう。CO₂を含むガス分子の吸着・分離の研究における固体NMRの利用が盛んになれば，多孔性材料の開発・応用の更なる進展につながると期待される。