日本ゼオライト学会　刊行物 Publication of Japan Zeolite Association

多孔体への吸着を用いた混合ガスの分離プロセスにおいて，混合ガスに水蒸気が含まれる場合，しばしば分離したいガスと水蒸気との間で競争吸着が生じる。このとき，競争的に水が吸着すると分離性能が著しく低下することが知られている¹⁾。その解決策として多孔体の表面疎水化が挙げられるが，多孔体表面に僅かにでも極性部位が存在する場合，その部位が水分子の吸着サイトとなる。そのため，疎水化だけでは水分子の競争吸着による吸着阻害を完全に防ぐことは難しい。このように，水蒸気の影響を防ぐためには水の吸着過程を理解したうえで，多孔材料の設計へ反映させることが重要である。

近年，多孔性材料への分子の吸着に関する研究は，吸着等温線や吸着熱および吸着速度といったマクロスコピックな物性を評価する手法に加え，コンピュータシミュレーションによるミクロスコピックな解析による物性の解明が盛んに行われている^2–4)。特にコンピュータシミュレーションの発展は，マクロ物性だけでは詳細に検討することが困難な，吸着分子の吸着サイト近傍での振る舞いや細孔内での運動状態のようなミクロな吸着状態の解明に大きく貢献している。この恩恵によってマクロとミクロが結び付けられ，吸着現象がより深く理解されている。一方で，古くから行われているマクロ物性測定を用いた研究は，測定法が十分に確立された等温過程での平衡状態に対するものが多いのに対して，等圧条件下で温度を変数とした吸着量の測定や非平衡状態である速度過程に対する研究は，特殊な測定が必要であるため，未解明な部分が多い。

等圧条件での測定は，吸着量と温度の関係である吸着等圧線の測定であり，吸着速度の検討において不可欠な拡散方程式の精密解を簡素化できる点で非常に魅力的である。またこれらの測定は，常温付近の温度変化に敏感で目的分子の吸着阻害を引き起こす水蒸気の競争吸着を研究するうえで強力な手段となりえる。しかし圧力一定条件での測定は，吸着に伴い気相から多孔体表面へのガスの物質移動が生じるため，常に圧力の変動を調整するシステムの構築が必要である。そのため吸着等温線を測定する通常の吸着装置と比べて装置構成が複雑になる。例えば重量法を用いた既存の吸着量の測定では，等圧制御自体は可能であるものの，大きな体積のチャンバーを必要とする重量天秤を用いるため，多孔性材料の温度や吸着質ガスの分圧の高精度な制御が難しい。また重量法では試料を天秤にかけるため，分光法^5,6)や散乱法^7,8)と組み合わせたin-situ測定が不可能である。そのため本研究では，重量法を用いない簡素化されたシステムで単成分ガスの等圧制御を実現する装置：圧力フィードバック法を開発した。

本稿では，筆者らの開発した装置の原理を説明するとともに，この装置を用いて疎水性シリカ材料（ZSM-5およびSBA-15）への水吸着を吸着等圧線および吸着速度の直接測定を行った研究について概説する。

吸着現象を理解するうえで最も重要な物理量である吸着量は，次式で定義される。

$$\begin{array}{}\text{(1)}& n=F{\left(P,T\right)}_E\end{array}$$

ここでnは吸着量，Pは平衡圧力，Tは平衡温度，およびEは固体表面と気体分子との相互作用を示す。式（1）は，固体と吸着する分子の組み合わせが決まっている場合，吸着量が圧力と温度の関数であることを示している。吸着等温線は，温度一定条件下での吸着量と圧力の関係を示しており，次式で定義される。

$$\begin{array}{}\text{(2)}& n=f{\left(P\right)}_{T,E}\end{array}$$

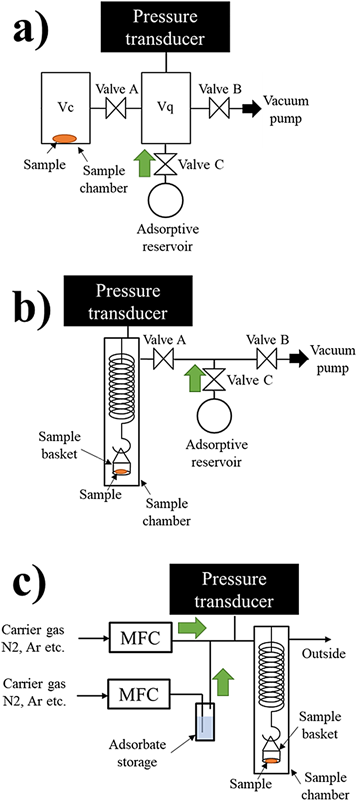
これより吸着等温線の測定は，圧力を変え吸着した気体の量を調べる測定であることがわかる。吸着量の決定は，吸着前後の気体の圧力変化より気体の状態方程式を用いて吸着量を決定する容量法，又は吸着媒の重量変化を直接測定して吸着量を決定する重量法を用いるのが一般的である。図1に最も簡単な容量法a）及び重量法b）の装置の概念図を示す。図1a），b）は閉鎖系であり吸着等温線の測定に用いる。一方，開放系の重量法：図1c）は，吸着性の極めて乏しいキャリアガスで希釈した分圧が一定の吸着ガスを流通して，平衡時の吸着量から吸着等圧線を得るのに用いる。

図1 容量法と重量法の概念図⁹⁾　a）：容量法，b）：閉鎖系の重量法，c）：開放系の重量法

吸着等圧線は，次式で定義される。

$$\begin{array}{}\text{(3)}& n=g{\left(T\right)}_{P,E}\end{array}$$

これより吸着等圧線の測定は，温度を変え吸着した気体の量を調べる測定であることがわかる。そのため実際の測定には，圧力を一定に制御する機構が必要である。しかし前節で取り上げた閉鎖系の容量法や重量法を用いた測定では，吸着により気相の圧力は減少し，また脱着によって圧力が増加するため，等圧条件での測定を行うことは不可能である。開放系の重量法測定は，チャンバー内を陽圧に保たなければならないという制限がある。特に後者については，吸着質に窒素やアルゴンといった通常キャリアガスとして用いられる気体に対して，1気圧以下で圧力制御を行うことが難しい。これらの問題を解決するためには，キャリアガスを用いない，単成分ガスを用いた等圧制御機構が必要である。これが圧力フィードバック法^10–12)である。

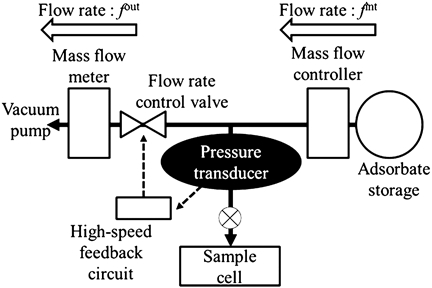
圧力フィードバック法の概念図を図2に示す。本装置の特徴は，装置上流部と下流部に取り付けられた二つの異なる流量制御システムである。本装置は次のようにして系の圧力の制御を行う。まず最上流部に取り付けたガス溜めから，微小かつ一定の流量f^intで系内に吸着質を導入する。そして，導入した気体の圧力を圧力トランスデューサーによって電気信号へ変換し，その信号を高速フィードバック回路へ伝達する。ここで圧力を一定に制御するためには，系内の圧力が目標圧力より高ければ排出流量f^outを高くし，また圧力が低ければf^outを低くする必要がある。この原理に基づき高速フィードバック回路は，流量制御バルブ（flow rate control valve）の開度を制御し，圧力変化に従いf^outを調整する。また等圧制御の安定性の向上のため，高速フィードバック回路は開度を一秒あたり約40回以上計算し，制御信号を流量制御バルブに伝達する。この機構によって，系内の圧力を一定にかつ目的の圧力に制御することが可能となる。さらに最下流部は真空ポンプで常に減圧しているため，1気圧以下の測定も可能である。

図2 圧力フィードバック法の概念図¹¹⁾

圧力一定条件における吸着量の算出は，圧力に対して独立な物理量を用いて行う必要がある。そのため圧力フィードバック法では，系内への導入流量および系外への排出流量を用いて吸着量を決定する^10–13)。等圧制御の際，系の物質収支は導入流量f^intおよび排出流量f^outの差より算出することが可能である。ある時間t_iにおける系の物質収支（dn^sys/dt_i）は次式で示される。

$$\begin{array}{}\text{(4)}& \begin{array}{c}\left(\frac{d{n}^{sys}}{d{t}_i}\right)＝k\left(f_i^{int}－f_i^{out}\right)＝k\Delta f_i\end{array}\end{array}$$

ここで，nは物質量，t_iは時間，kは換算定数，Δf_iは導入と排出の流量の差である。また系内の物質量変化は，気体の吸・脱着量（dn^ads/dt_i）と圧力変化に対応した物質量変化（dn^Press/dt_i）の和である。

$$\begin{array}{}\text{(5)}& \begin{array}{c}\left(\frac{d{n}^{sys}}{d{t}_i}\right)＝\left(\frac{d{n}^{ads}}{d{t}_i}\right)＋\left(\frac{d{n}^{Press}}{d{t}_i}\right)\end{array}\end{array}$$

この時，圧力一定であれば（dn^Press/dt_i）=0となり式（4），（5）より，

$$\begin{array}{}\text{(6)}& \begin{array}{c}\left(\frac{d{n}^{ads}}{d{t}_i}\right)＝k\Delta f_i\end{array}\end{array}$$

となる。この関係から，流量の差分を数値的に時間積分することで吸着量を決定することが可能である。よって吸着量n^adsは，

$$\begin{array}{}\text{(7)}& \begin{array}{c}{n}^{ads}＝ k{\displaystyle {\int }_{t_0}^{t_j}\Delta fdt}\simeq k{\displaystyle \sum }_{i＝0}^j\Delta f_i\Delta t_i\end{array}\end{array}$$

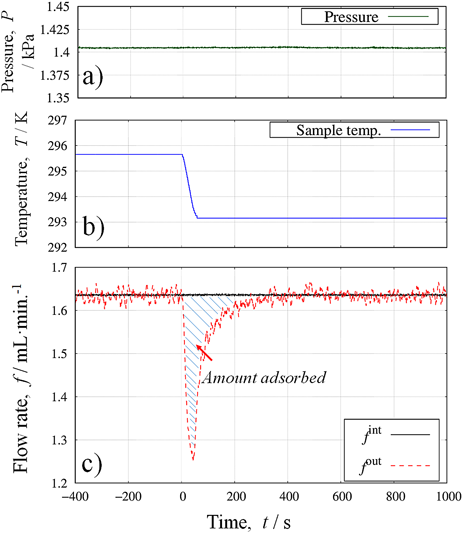
となる。図3に，等圧線測定において圧力を1.41 kPaに制御し，試料温度を295.75 Kから293.25 Kに変更したときの圧力，温度および導入・排出流量の時間変化を示す。平衡温度を変更した時点を時間t=0としている。図3a）より，試料温度を変えても圧力が一定に制御されていることがわかる。またこの時の吸着量（Amount adsorbed）は，図3c）に示す導入量と排出流量の差の面積に相当する。この決定手法を用いれば圧力一定条件において，平衡温度を段階的に変え吸着量を測定することで，吸着等圧線を得ることが可能である。また圧力フィードバック法の精密な圧力制御を利用すれば，段階的に圧力を変化させ，正確に制御された目的圧力における吸着量を測定することも可能である。さらに現在では多成分系への拡張も行っている。

図3 Na-ZSM-5を用いた水吸着実験における圧力，温度および流量の測定例　a）：圧力の時間変化，b）：サンプル温度の時間変化，c）：導入および排出流量の時間変化

速度論的な気体吸着の解析は，等温過程における吸着量の時間変化に対して拡散方程式に基づいた数学的モデルを用い，拡散係数や速度定数などの速度論的パラメータを決定する手法が一般的である。表1にFick拡散方程式の精密解および，線形推進力近似モデル（Linear driving force model: LDF）を示す。速度論的パラメータの抽出を行う上で，適用するモデルは圧力が一定か，体積が一定かで異なり，実験に適したモデルを選択する必要がある。一般的な測定例として，圧力一定条件では図1c）に示す分圧制御型の重量法を用いる場合が多く，また体積一定条件では気相の圧力変化が無視できるほどの大きな気体導入体積を持つ容量法を用いる必要がある。重量法の測定では，吸着熱が測定に及ぼす影響を抑えるために試料量に制限があり，キャリアガスの競争吸着の影響を皆無にすることが難しい。さらに容量法を用いる場合は，等圧条件に比べフィッティングパラメータが増え計算コストを要するといった解析面での問題や大きな気体導入体積を一定温度に制御するといった測定面での困難さが生じる。これらの問題を解決するためには，単成分の気体吸着質の圧力制御機構を備えた小体積の吸着システムが必要であり，筆者らの開発した圧力フィードバック法はこの条件を十分に満たす。

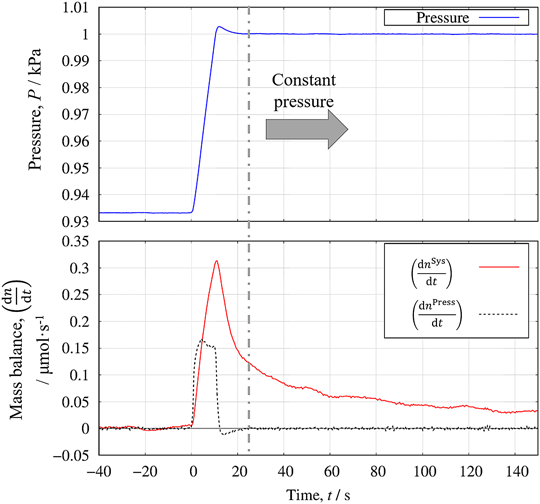
次に圧力フィードバック法を用いた吸着速度パラメータの決定について述べる。図4a），b）に等温過程において水蒸気吸着等温線を測定した際に，平衡圧力を0.93 kPaから1.00 kPaへ変更した際の圧力および物質収支の時間変化を示す。時間t_iにおける系の物質収支（dn^sys/dt_i）は，導入流量と排出流量の差分より求め，圧力変化による物質収支（dn^Press/dt_i）は，圧力の時間変化を数値微分することで算出している。時間t=0は圧力を変化させたときの時間を示す。ここでt=0において設定圧力を変化させると，系の圧力は約30秒以内に目的圧力に到達し，それ以降は一定の値を示すことがわかる。この時，系内の物質収支（dn^sys/dt_i）は，式（5）によって表されるから，式（8）に示す通り系の物質収支は吸着速度r_i^adsに相当する。

$$\begin{array}{}\text{(8)}& \begin{array}{c}\left(\frac{d{n}^{sys}}{d{t}_i}\right)＝\left(\frac{d{n}^{ads}}{d{t}_i}\right)＝ r_i^{ads}\end{array}\end{array}$$

この吸着速度の実測は，微分量である流量を吸着量決定に採用した圧力フィードバック法により初めて成功したものである。また表1に示す速度モデルの時間に対する微分式を用いることで，吸着速度定数や拡散係数を決定することが可能である。

図4 SBA-15への水吸着実験における圧力および物質収支の時間変化　a）：圧力，b）：圧力変化および吸着による物質収支

従来の重量法は，吸着量M（t_i）の時間変化から吸着速度パラメータを決定していた。この方法では，前述した温度の影響や大きな体積に対する分圧制御の精度に対する懸念を拭い去ることは難しい。しかし圧力フィードバック法では，装置を小型化し，温度制御に特化した試料セルを搭載することが出来るため，迅速な圧力制御と精密な温度制御が可能である。

さらに本手法の特徴として，クライオスタットを用いることで極低温領域での吸着速度および吸着量を測定できることが挙げられる。低温での1気圧を下回る圧力範囲での測定も圧力フィードバック法を用いて解析できる。

本節では，圧力フィードバック法を用いて測定した吸着等圧線測定の研究成果と共にその有用性について述べる。

疎水性ナノ空間内では，水分子がクラスターを形成し，ナノ空間を充填する^17,18)。またシミュレーションによる結果では，クラスター形成に親水的な吸着サイトが重要な役割を果たすことが示されている。この研究では吸着サイトの量を制御し合成することができるZSM-5¹⁹⁾を用いて水の吸着実験を行った。ZSM-5の骨格を成す≡Si－O－Si≡のシロキサン架橋構造は，同じ骨格構造を成すsilicalite-1の水吸着等温線がV型を示すように，SiとO間における電気的な偏りを考慮しても疎水的である²⁰⁾。一方でZSM-5骨格中に含まれるAl近傍に存在する交換性カチオンは，静電相互作用により強く水分子を吸着する。またSi/Al比の低いZSM-5では，細孔表面の交換性カチオン密度が高くなるため，吸着した水分子を表面に引き付ける静電相互作用の強度が増す。これはSi/Al比の違いにより，ZSM-5の親水性が異なることを示唆している。そのためZSM-5は疎水性ミクロ孔内での水分子吸着に対する吸着サイトの影響を調べる上で非常に良いナノ空間モデルと成りえる。

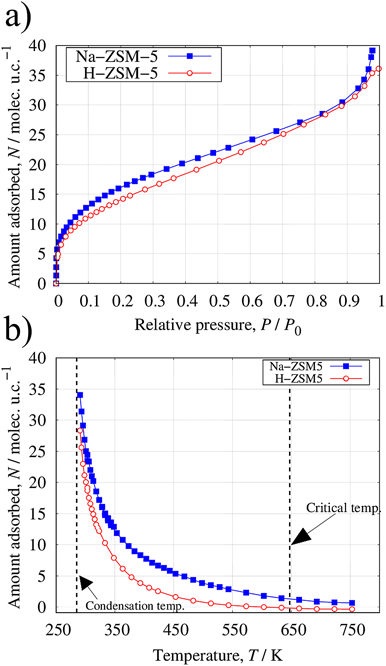
Na-ZSM-5は合成したものを使用した。またNa-ZSM-5よりイオン交換と焼成を経てH-ZSM-5を得た。等温線および等圧線測定の試料前処理は，P<1 mPa，T=723 Kにおいて6時間で行った。図5a）に容量法を用いて303 Kで測定したSi/Al=25のNa-ZSM-5およびH-ZSM-5の水吸着等温線を示す。等温線は，低圧で急激に吸着量が増加し，中圧から高圧にかけて吸着量が直線的に増加した。低圧における急激な吸着量の増加は，固体表面と水分子との親和性が高いことを示している。D. H. Olsonら¹⁷⁾は，P/P₀≤0.05での圧力上昇に伴う急激な吸着量の増加は，H-ZSM-5のブレンステッド酸点への吸着であることを示しており，Na-ZSM-5においてもNaカチオンを取り囲むように水分子が吸着すると考えている。D. H. Olsonら²¹⁾やT. Sanoら²²⁾の方法を用いて等温線より吸着サイト当たりの吸着量を求めると，Na-ZSM-5では4.4分子，H-ZSM-5では3.5分子であり，Naカチオンの方が多くの水分子をサイト周りに引き付けている。

図5 Na-ZSM-5およびH-ZSM-5の水吸着等温線および等圧線¹⁰⁾　a）：303 Kにおいて測定した等温線，b）：1.4 kPaにおいて測定した等圧線

図5b）には同じ試料を用いて水蒸気圧1.4 kPaにおいて測定した水の吸着等圧線を示す。Na-ZSM-5およびH-ZSM-5の水吸着等圧線は，凝縮温度に近い低温において最大値を示し，温度上昇に伴い指数関数的に単調に減少する。また水和数に対応する吸着量（ZSM-5の単位格子当たり約10分子以下）において，Na-ZSM-5はH-ZSM-5に比べ，最大で150 K以上高い温度まで細孔内に水を保持することが明らかとなった。この結果より，疎水性ナノ空間における水和構造の熱的安定性は，カチオン種によって大きく異なり， Naカチオンがプロトン（ブレンステッド酸点）に比べ非常に強い相互作用で水分子を吸着していることがわかる。この様な吸着サイトであるカチオン種の影響は，等温線測定を行うことでも確認できる。しかしその場合，極めて低圧部の測定を要するために低圧に特化した高精度な圧力計が必要となり，圧力の測定精度といった装置上の問題に直面する。一方で等圧線測定では，汎用的な圧力計により1.4 kPaと比較的高い圧力において，温度を変数として測定するだけで吸着サイトと吸着質分子との相互作用の違いを定性的に明らかにすることが可能である。また強い相互作用で吸着が生じる系では高温において吸着量の差が顕著となるため，より有効的な測定手法であると言える。吸着質分子と吸着媒との相互作用を詳細かつ定量的に議論するには，異なる温度で測定した等温線より，クラウジウス-クラペイロン式を用いて等量吸着熱を評価する方法，また，マイクロカロリメータを用いた微分吸着熱測定を行う方法がある。しかし，吸着等圧線は比較的簡易な装置で短い時間で測定することが可能であり，その結果から定性的な相互作用の違いや一定圧力下での温度と吸着量の関係が得られ，工業的な試験として有用である。また類似測定であるTG法は，サンプルセル周りの精密な分圧制御を行えない点や平衡測定における低い吸着量の定量性から正確な吸着等圧線を測定することは難しい。

気体吸着法の中で最も一般的な測定は，液体窒素を冷媒に用いた窒素吸着である。しかし，近年の技術革新に伴い，低温液体の代わりにクライオスタットを用い吸着等温線を測定する技術が進歩した。液体窒素に代表される低温液体は，その沸点における測定試料の温度制御に使用される。しかし常圧で低温液体となる分子種が限られるため，温度を自在に可変することは困難であり，測定温度は限定される。さらに液体が蒸発してしまうので測定時間が制限されるといったデメリットがある。そのため近年では，低温液体を用いないHeコンプレッサー式のクライオスタットを用いた手法が開発された。クライオスタットを用いた吸着実験では，試料温度の制御が可能である。しかしその反面，天秤のような比較的大きな機構を冷却することは困難であり，クライオスタットは容量法でのみ使用されることが多く，動的な吸着測定に用いられることは稀である。そこでこの研究では，圧力フィードバック法にクライオスタットを搭載した試料セルを用い低温度領域での吸着速度測定を行った。

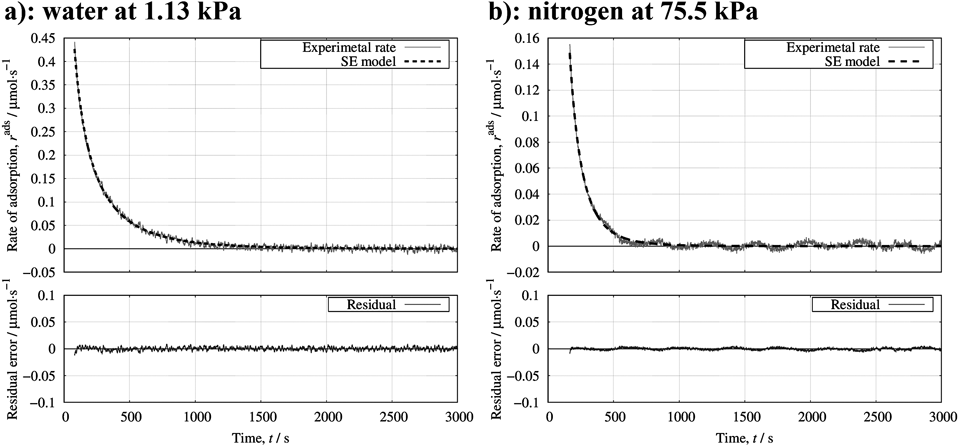
この研究では合成したメソポーラスシリカSBA-15を用いて，無極性分子である窒素分子（77 K）と極性分子の水分子（298 K）の吸着速度を測定し速度定数を決定した。その決定には表1に示すLDFモデルの派生モデルであり緩和時間の分布を考慮したStretched Exponentialモデル（SEモデル）²³⁾を用いた。

$$\begin{array}{}\text{(9)}& r_i^{\text{ads}}=M_e{k}^{\beta }\beta t^{\beta -1}\exp \left[-{\left(k{t}_i\right)}^{\beta }\right]\end{array}$$

ここでMe：平衡吸着量，k：速度定数，β：exponential factorを示す。理論関数によるフィッティング結果を図6に示す。測定した吸着速度の時間変化は，吸着で用いられる速度式で十分に再現することができ，吸着速度測定の妥当性を示している。また本手法では，従来から速度定数の決定に用いられてきた吸着量の時間変化ではなく，吸着速度の時間変化を用いて速度定数を決定する。従来の方法では，吸着量が平衡に達するまで吸着量の時間変化を測定する必要があった。しかし吸着速度を用いる場合では，速度が無限時間経過後0に漸近することを考慮すれば，短い時間での吸着速度データ収集で速度定数を推算することが可能である。そのため，特に圧力スイング法のような一度の圧力変化を印加する様な吸着プロセスにおいて，圧力フィードバック法を用いることで短時間での正確な吸着速度定数決定が可能である。

図6 SBA-15への水および窒素吸着速度の時間変化　a）：298 K 1.13 kPaにおける水の吸着速度　b）：77 K 75.5 kPaにおける窒素の吸着速度

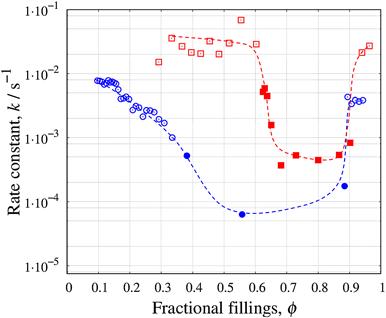
次に速度定数と細孔充填率の関係を図7に示す。吸着実験の試料前処理は，P<1 mPa, T=393 Kにおいて6時間で行った。窒素吸着の速度定数は，細孔内表面への吸着に対応する細孔充填率0.3<φ< 0.6の範囲において10⁻²/sのオーダーで一定の値を示し，毛管凝縮が起こる0.6≤φ≤0.9において細孔表面吸着の1/80程度である4×10⁻⁴/sまで減少した。一方で水吸着の場合，細孔内表面吸着が起きる0.1≤φ≤0.35では，φの増加に伴い速度定数が8×10⁻³/sから1×10⁻³/sまで約一桁単調に減少し，毛管凝縮が起きるφ=0.55で6×10⁻⁵/sと最小になった。この結果より，水吸着の測定温度は，窒素吸着の測定温度に比べて極めて高い温度であるにもかかわらず，水分子の吸着速度定数は窒素吸着の1/10程度であることが明らかとなった。律速過程が窒素分子や水分子の気体拡散であると仮定した場合，測定の圧力や温度における吸着する分子の平均自由行程lと平均細孔径w̅の割合がw̅/l≤0.1のときはKnudsen拡散が支配的で，10≤w̅/lの時は分子拡散が支配的である。本測定条件において，窒素を用いた場合では0.08≤w̅/l≤0.4であり，水の場合では3×10⁻⁴≤w̅/l≤2×10⁻³と両者においてKnudsen拡散が支配的であると考えられる。しかし実際に窒素と水のKnudsen拡散を計算すると，水のD_k^waterは窒素のD_k^nitrogenの2.45倍となり測定結果と矛盾する。この結果は，律速過程がもはや気体拡散では説明できないことを示し，吸着相の形成過程を考慮した動的な吸着メカニズムが律速となりえることを示唆している。

図7 SBA-15への水および窒素吸着速度定数¹³⁾（□および■：298 Kにおける水吸着速度定数，○および●：77 Kにおける窒素吸着速度定数，open key：表面吸着，solid key：毛管凝縮）

本稿では次世代型の吸着測定システムである圧力フィードバック法の開発とそれを用いた吸着量や吸着速度の測定法を実際の測定例と合わせて概説した。圧力フィードバック法は，単成分ガスを用いた二種類の異なる流量制御システムを採用することで，等圧制御と同時に吸着量を測定することが出来る装置である。また装置の簡便さから，極めて小体積での圧力制御が可能であり，精密な圧力制御や吸着速度測定を行うことが可能である。

圧力フィードバック法を用いて可能となった吸着等圧線測定は，ゼオライトの交換性カチオンと水分子といった強い相互作用によって生じる吸着機構を研究するのに優れた測定である。また圧力一定での吸着量と温度の関係は，実用プロセスとして吸着を用いる場合に重要な知見となりえる。吸着速度測定では，圧力フィードバック法を用いることで，今まで難しかった単成分ガスを用いた吸着速度定数の決定に成功した。本装置はその機構上，試料セルの形状が限定されないという利点がある。そのため，動的吸着測定では今まで使用されることが稀であったクライオスタットを用いた測定が可能であり，低温におけるガスの動的吸着メカニズムを解明することが可能である。さらにこの利点より，散乱法や分光法のin-situ測定へ応用による，動的なミクロ吸着挙動の解明が期待できる。