日本ゼオライト学会　刊行物 Publication of Japan Zeolite Association

2–50 nmのメソ細孔を有する多孔体では，バルクの飽和蒸気圧よりも低い圧力において毛管凝縮が生じることが知られている。毛管凝縮が生じる圧力は細孔径に強く依存し，メソ多孔体の細孔径分布評価の指標として用いられることから，現象の詳細な理解が必要不可欠である¹⁾。メソ多孔体の中でも特に，MCM-41²⁾やSBA-15³⁾に代表される両端開放型規則シリカ多孔体においては，しばしば吸着ヒステリシス―毛管凝縮／蒸発が異なる圧力で生じる現象―が観測される。Fig. 1に示す細孔径の異なるMCM-41におけるAr吸着等温線^4–6)からわかるとおり，吸着ヒステリシスは細孔径が小さくなるにつれ（またここでは示さないが温度が高くなるにつれ），その幅が小さくなり，やがて消滅する。この吸着ヒステリシス挙動については古くから多くの検討がなされており，毛管蒸発（脱着過程）が平衡相転移である一方，毛管凝縮（吸着過程）は核生成を伴う準安定状態からの相転移であることが，吸着ヒステリシスが生じる原因であると報告されている⁷⁾。しかし，MCM-41が初めて合成されてから20年を経た現在においても，定性的なメカニズムの提案に留まっており，ヒステリシスが消失する臨界温度や臨界細孔径，さらには準安定状態から生じる毛管凝縮圧の予測を与えるような定量的な説明はなされていない。この問題が未解決である原因として，多分子層吸着状態（凝縮前）から凝縮状態（凝縮後）への非平衡遷移過程に関する速度論的な理解の欠如が挙げられる。そこで我々は，分子シミュレーションを援用しつつ毛管凝縮過程の自由エネルギー変化およびエネルギー障壁を求め，さらには，これらをもとに毛管凝縮の速度定数を評価することで，毛管凝縮／吸着ヒステリシス機構の速度論的な理解を試みた⁸⁾。本稿では，用いたシミュレーション手法や，得られた結果について解説する。

Fig. 1 Argon adsorption isotherms at 87 K on the MCM-41 materials with pore diameter of 3.13⁴⁾, 4.15⁵⁾, and 5.54 nm⁶⁾. P_eq is the thermodynamic equilibrium phase transition pressure, calculated through the gauge cell Monte Carlo simulations by Vishnyakov and Neimark⁷⁾.

2.1. Atomisticシリカ多孔体モデル構築

従来，細孔表面原子をあらわに考えない理想的なシリンダー型細孔モデルを用いた分子シミュレーションにより，吸着挙動や毛管凝縮挙動の理解が試みられてきたが，近年，実際の規則シリカ多孔体の細孔表面には原子オーダーのラフネスが存在することが明らかにされている⁹⁾。比較的小さな細孔ではこの表面ラフネスが毛管凝縮挙動に与える影響を無視できないことから，シミュレーション結果と実験結果とを厳密に比較するためには，ラフネスを考慮したAtomisticな規則シリカ多孔体モデルの構築が必要である¹⁰⁾。そこで本研究では，X線構造解析により得られるMCM-41の細孔壁近傍の電子密度分布⁹⁾をもとに，Atomisticモデルを構築した。

まずは，分子動力学（Molecular dynamics; MD）法によりアモルファスシリカブロックを構築した。MD法は，設定された分子間の相互作用ポテンシャルをもとに分子間に働く力を計算し，分子集団系の運動方程式を解くことでそれぞれの分子の軌道を求める手法である。今回採用したBKSポテンシャル¹¹⁾は，Si–Oが四面体構造をとる時に最安定となるような相互作用ポテンシャルであり，これに従いクエンチMDシミュレーションを行うことでアモルファスシリカが自然と構築される。得られたアモルファスシリカブロックを円筒状にくり抜き，最後に，MCM-41のX線構造解析から得られる細孔壁近傍の電子密度分布を満たすように，細孔表面のSiおよびO原子をランダムに削除・再生していくことでAtomisticシリカ多孔体モデルを構築した。なお，実際の規則シリカ多孔体の細孔表面O原子はH原子と結合し水酸基として存在していると考えられるが，H原子はサイズが小さく，Arなどの希ガス吸着分子との相互作用は無視できるため，本研究ではH原子を考慮していない。得られたAtomisticモデルは，低圧における吸着シミュレーションにより細孔表面への吸着状態を良好に再現できること，また，中性子散乱スペクトルが実験結果に符合していることから，その妥当性が示されている^10,12)。

2.2. Ar吸着シミュレーション｜grand canonical Monte Carlo法

構築したAtomisticモデルに加え，古くから用いられている細孔表面原子をあらわに考えない滑らかなシリンダー型細孔モデル¹³⁾を用いてAr吸着シミュレーションを行った。二体間相互作用ポテンシャルuにはLennard–Jones（LJ）12–6ポテンシャル，$$\begin{array}{}\text{(1)}& u＝－4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}－{\left(\frac{\sigma }{r}\right)}^6\right]\end{array}$$

を用いた。ここで，rは分子間距離，σは分子の大きさを特徴づけるパラメータ，εは相互作用の強さを特徴づけるパラメータである。三体間相互作用などの多体間相互作用は無視し，系全体のポテンシャルエネルギーは二体間相互作用の和で表せるとした。吸着シミュレーション手法にはgrand canonical Monte Carlo（GCMC）法を用いた。MD法では分子集団の運動方程式を解き，時々刻々得られる微視的状態（つまり全分子の位置および速度）から，物理量（例えば全エネルギー）を計算し，その時間平均を求めることで平衡状態における系の物理量を計算することができる。一方Monte Carlo（MC）法では，統計力学により記述される配置の出現確率に従うよう，分子集団の微視的状態（つまりは全分子の座標）をランダムに発生させ，それぞれの微視的状態における物理量の平均（アンサンブル平均）を求めることで，平衡状態における系の物理量を計算することができる。特にGCMC法は，化学ポテンシャルμの粒子浴，温度Tの熱浴と接した体積Vの分子集団（grand canonicalアンサンブル）の平衡状態の描像を与える。具体的には，細孔セルにおいて吸着分子の挿入・移動・削除試行を行い，試行前後のポテンシャルエネルギー変化とμ，V，Tで決まる統計力学に基づく確率分布から，各試行のAccept/Rejectを判断する。Acceptの場合は系の微視的状態が更新され，Rejectの場合は試行前の状態に戻る。これをおおよそ10⁵/atomステップ繰り返し，各ステップにおける物理量（エネルギーや分子数）の平均値をもとめることで，μ，V，Tで規定される平衡状態の情報を得ることができる。化学ポテンシャルμのバルク気相の圧力Pは，LJ流体の状態方程式や，Widomの分子挿入法¹⁵⁾を適用した分子シミュレーションにより容易に計算可能であるため，種々のμにおけるGCMC法により細孔セル内の分子数Nを求めることで，吸着等温線（P vs. N at constant T）を計算することができる。

毛管凝縮は，細孔内における凝縮核生成を必要とする活性化過程であり，その遷移状態は自由エネルギー的に不利な状態，つまりは統計力学に基づく確率論的に「発生しにくい」状態である。GCMC法は計算時間の制限があるため，実験的に観測される毛管凝縮圧P_condではエネルギー障壁を乗り越える（つまり確率的に発生しにくい遷移状態を観測する）ことができず，結果，エネルギー障壁が十分に低くなる，より高い圧力P_cond^GCMC（>P_cond）において毛管凝縮が観測される¹²⁾。したがって，GCMC法のみでは毛管凝縮のような活性化過程を含む現象を定量的に理解することが困難であり，ましてやその温度，細孔径依存性を予測することは不可能である。そこで，以下に述べるような自由エネルギーを媒介にした速度論的な検討が必要となる。（GCMC法の計算ステップ数や分子数を十分に多くすることで，P_condを直接予測することも原理的には可能であると期待されるが，増やすべきステップ数が膨大であるため現実的ではない。どれほどのステップ数が必要であるかについても後ほど議論する。）

2.3. Gauge cell Monte Carlo法

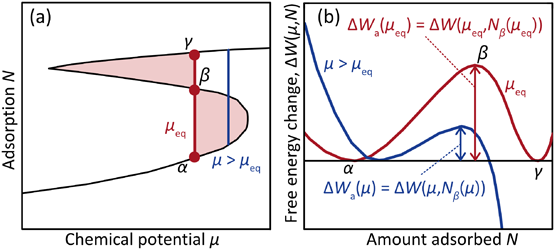
凝縮のエネルギー障壁を見積もるためには，多分子層吸着状態と凝縮状態の中間状態を解析せねばならない。そこで，体積V_poreの細孔セルと体積V_gasのバルク気相セル（gaugeセル）の二つのシミュレーションセルを用意し，全系において分子数N，体積V=V_pore+V_gas，温度T一定のもと，セル内，セル間の分子の移動試行を繰り返すシミュレーション手法であるgauge cell Monte Carlo法¹⁶⁾によりFig. 2aに示すような連続なS字型の吸着等温線（van der Waalsループ）を計算した。種々のNにおいてシミュレーションを実施し，細孔セルに存在する分子数およびバルク気相セルにおいて計算される系の化学ポテンシャルから吸着等温線が計算される。この手法もGCMC法同様，NVTの条件（canonicalアンサンブル）から統計力学の原理により決定される確率分布を満たすように，試行のAccept/Rejectが行われる。一方，GCMC法とは異なり，系の分子数Nを固定し，細孔に流入する分子数のゆらぎを制限することで，実際の吸着等温線測定では観測し得ない，絶対不安定領域を経由するS字型の吸着等温線を計算することができる。この等温線は連続であるため，吸着量を化学ポテンシャルで積分することで系の自由エネルギーを計算することが可能になる。

Fig. 2 Schematic representation of the (a) sigmoid adsorption isotherm calculated via the gauge cell MC method and (b) free energy associated with the adsorption process. The equilibrium phase transition point μ_eq is obtained by applying the Maxwell rule of equal areas (filled red areas in (a))to the sigmoid isotherm.

得られたS字吸着等温線にMaxwellの等面積則を適用することにより，平衡転移点μ_eqを求めた。μ_eqは多分子層吸着状態（凝縮前）と凝縮状態（凝縮後）の自由エネルギーが等しい点であり，つまりは熱力学的に決定される平衡論的な毛管凝縮圧を表す。

多分子層吸着状態α（分子数N_α）を基準とした，ある状態（分子数N）の自由エネルギーΔW(μ, N)を，以下の式¹⁷⁾に従ってS字等温線μ_s(N)を積分することで求めた。$$\begin{array}{}\text{(2)}& \Delta W\left(\mu ,N\right)＝{\displaystyle {\int }_{N_{\alpha }}^N{\mu }_s\left(N^{\prime }\right)}d{N}^{\prime }－\mu \left(N－N_{\alpha }\right)\end{array}$$

毛管凝縮のエネルギー障壁ΔW_a(μ)は，多分子層吸着状態αから遷移状態β（分子数N_β）へ変化する際の自由エネルギー変化で表されることから，ΔW_a(μ)=ΔW(μ, N_β)により計算される。μ_eqにおける自由エネルギー変化ΔW(μ_eq, N)をFig. 2bに示す。多分子層吸着状態αと凝縮状態γの自由エネルギーは確かに等しく，また，毛管凝縮過程には遷移状態βが存在することがわかる。さらに，μが大きくなるにつれ（つまり，圧力Pが高くなるにつれ），エネルギー障壁が低くなっていることが確認できた。

2.4. 毛管凝縮の速度定数｜遷移状態理論

毛管凝縮のエネルギー障壁がもたらす速度論を理解すべく，速度定数k(μ)を求めた。活性化過程を記述する遷移状態理論^18,19)によると，k(μ)は，$$\begin{array}{}\text{(3)}& k\left(\mu \right)=Cp\left(\mu \right)\end{array}$$

ただし，$$\begin{array}{}\text{(4)}& C＝\frac{1}{2}\langle \frac{dN}{dt}|{}_{N＝N_{\beta }}\rangle \end{array}$$$$\begin{array}{}\text{(5)}& p\left(\mu \right)＝\frac{\exp \left[－\frac{D}{L_z}\frac{\Delta W_a\left(\mu \right)}{k_{B}T}\right]}{{\displaystyle {\int }_0^{\frac{D}{L_z}{N}_{\beta }\left(\mu \right)}\exp \left[－\frac{D}{L_z}\frac{\Delta W\left(\mu ,N\right)}{k_{B}T}\right]}dN}\end{array}$$

ここで，Cは遷移状態βにおける平均吸着速度，p(μ)は遷移状態βが発現する確率，Dは細孔径，L_zは細孔軸方向のシミュレーションセル長さを表す。なお，p(μ)の分子は遷移状態βにおける微視的状態数，分母は分子数0の状態から分子数N_βの状態までの全ての微視的状態数の総和を表す。ここで，p(μ)に含まれるN_β, ΔW_a(μ)，ΔW(μ, N)はシミュレーションセルの長さL_zに比例する量である。したがって，毛管凝縮現象を的確に捉えるためには，毛管凝縮の特徴長さLを決定し，このLあたりのN_β，ΔW_a(μ)，ΔW(μ, N)を考える必要がある。VishnyakovとNeimarkによると⁷⁾，毛管凝縮は細孔の内部で液ブリッジが生成することがきっかけで進行し，この液ブリッジの長さがおおよそ細孔径D程度であることから，毛管凝縮の特徴長さLは細孔径Dであると提案している。そこで本研究においても式（5）に示すように，DあたりのN_β，ΔW_a(μ)，ΔW(μ, N)を用いてp(μ)を求めた。遷移状態βにおける平均吸着速度Cは細孔内への吸着分子の拡散速度により決定されると予想される。ナノスケールの細孔では，分子拡散よりもクヌーセン拡散が支配的であり，クヌーセン拡散係数は$$\begin{array}{}\text{(6)}& D_K=\frac{1}{3}D\sqrt{\frac{8k_{B}T}{\pi m}}\end{array}$$

で表される。ただしmは分子量である。これから，本研究で対象とする2–8 nmの細孔径および75–100 Kの温度範囲では，ナノ細孔内での拡散速度のオーダーは変わらないことがわかる。後に議論するとおり，毛管凝縮圧を予測するためには，速度定数の詳細な値ではなく，そのオーダーが重要になるため，本研究ではCは温度，細孔径によらず一定であると見做し，無次元速度定数k*(μ)=k(μ)/C=p(μ)を用いて議論を行う。

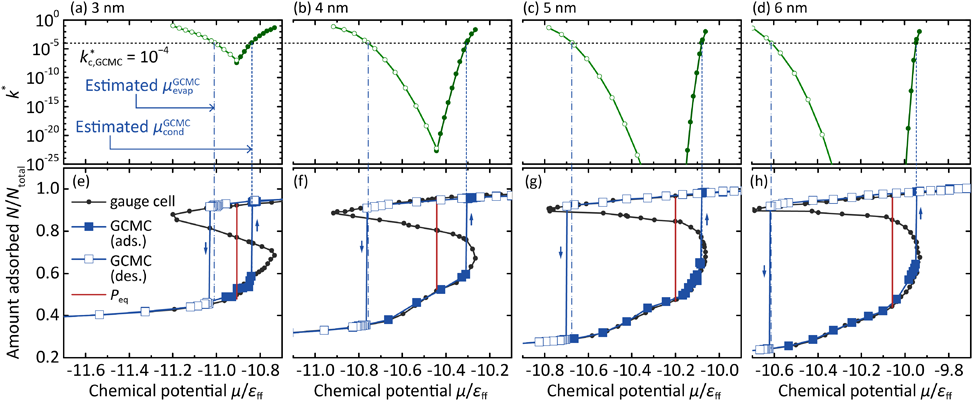
3.1. GCMC系における毛管凝縮圧の予測

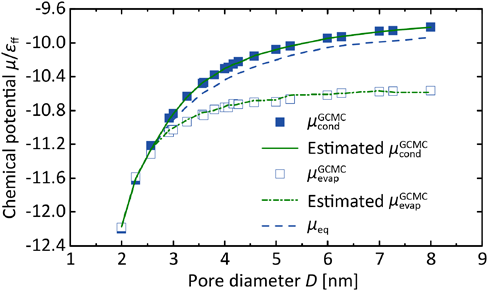
Fig. 3a–dに細孔径D=3.0, 4.0, 5.0, 6.0 nmの滑らかなシリンダー型細孔モデルを用いて求めた無次元速度定数の化学ポテンシャル依存性を示し，Fig. 3e–fには，同じ細孔モデルを用い，GCMC法およびgauge cell MC法により計算した87 KにおけるAr吸着等温線を示す。平衡転移点μ_eqにおける速度定数k*(μ_eq)は，D=3.0, 4.0, 5.0, 6.0 nmでそれぞれ，10⁻⁸，10⁻²³，10⁻⁴⁸，10⁻⁷²となった。この結果は，μ_eqでは毛管凝縮が遅すぎる（つまり発生する頻度が低すぎる）ために，GCMCシミュレーションの計算時間内に毛管凝縮が観測されなかったことを示唆している。そこで，「GCMCシミュレーションの計算時間内に毛管凝縮を観測し得る十分に速い速度」を表す臨界速度定数k*_{c, GCMC}を以下のように決定した。Fig. 3eのD=3.0 nmを用いたGCMCシミュレーション結果に着目すると，毛管凝縮はμ_cond^GCMC/ε_ff=−10.84で生じており，また，Fig. 3aに示すとおり，このμ_cond^GCMCにおける速度定数はk*(μ_cond^GCMC)=10⁻⁴であった。この結果より，GCMCシミュレーションにおける臨界速度定数をk*_{c, GCMC}=10⁻⁴と決定した。D=4.0, 5.0, 6.0 nmにおいて，速度定数がこの臨界速度定数と等しくなる化学ポテンシャルを探索し（Fig. 3b–d），これを予測毛管凝縮点μ_cond^GCMCとしたところ，シミュレーション結果を良好に再現できた（Fig. 3f–h）。さらに，Fig. 4に示すとおり，k*_{c, GCMC}=10⁻⁴を用いることで2–8 nmの幅広い細孔径においてGCMCシミュレーションにより計算されるμ_cond^GCMCを予測することに成功した。

Fig. 3 Dependences of the dimensionless rate constant for capillary condensation/evaporation on the chemical potential for pores with D= (a) 3.0, (b) 4.0, (c) 5.0, and (d) 6.0 nm. Open symbols: desorption process and closed symbols: adsorption process. Argon adsorption isotherms at 87.3 K obtained using the GCMC and gauge cell MC methods for pores with D= (e) 3.0, (f) 4.0, (g) 5.0, and (h) 6.0 nm.

Fig. 4 Pore size dependence of the chemical potentials for capillary condensation and evaporation in the GCMC system. The estimated μ_cond^GCMC and μ_evap^GCMC values were obtained using k*_{c, GCMC}=10⁻⁴.

両端が解放されたシリンダー型細孔内で凝縮している液体が蒸発する場合，気泡核の生成を必要とせず，細孔入口のメニスカスが単に後退することで進行するため，緒言でも述べた通り毛管蒸発は，通常，平衡な相転移挙動となる。しかし，本研究におけるGCMCシミュレーションでは，周期境界条件により無限に長い細孔を想定していることから，蒸発が進行するためには細孔内での気泡核の生成が必要となる。結果として，Fig. 3e–hに示すとおりGCMCでの毛管蒸発は準安定状態（μ_eqよりも低いμ）からの非平衡相転移となる。そこでμ_cond^GCMC同様，k*_{c, GCMC}=10⁻⁴により毛管蒸発点μ_evap^GCMCの予測を試みた。予測したμ_evap^GCMCはシミュレーション結果と良好に一致しており（Fig. 3e–hおよびFig. 4），これらの結果は，k*_{c, GCMC}=10⁻⁴がGCMCシミュレーションにおける臨界速度定数として妥当であるということを裏付けるものであると言える。

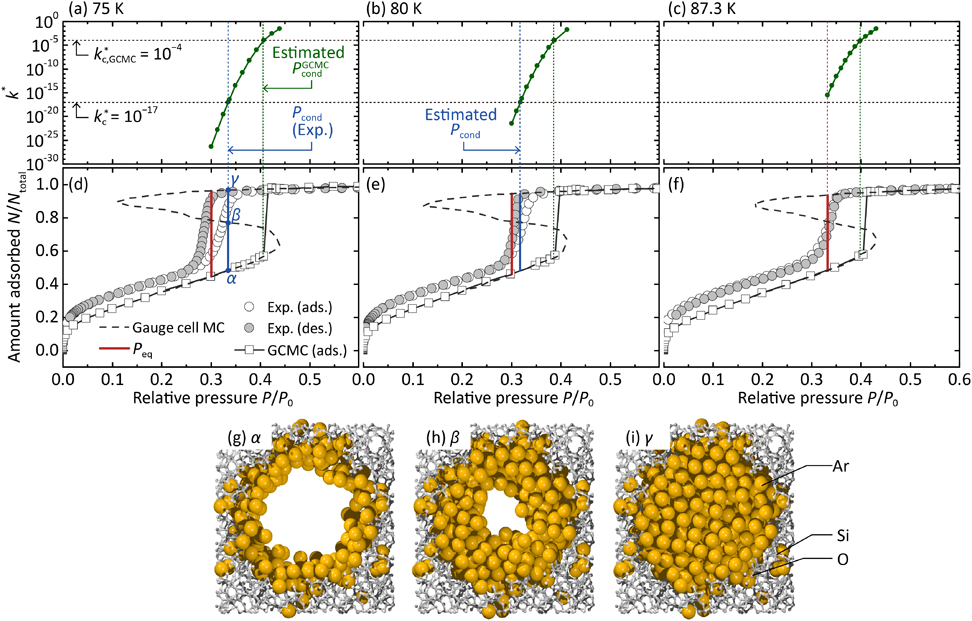
さらに，Atomisticモデルにおけるk*_{c, GCMC}=10⁻⁴の適用可能性も検証した。Fig. 5a–cにはそれぞれ，MCM-41（細孔径3.3 nm）を模したAtomisticモデルを用いて計算した毛管凝縮の速度定数の，75, 80, 87 Kにおける圧力依存性を示し，Fig. 5d–fにはそれぞれ，同じ細孔モデルを用いてGCMC法およびgauge cell MC法により計算した75，80，87 KにおけるAr吸着等温線を示す。全ての温度において，k*_{c, GCMC}=10⁻⁴により予測されるμ_cond^GCMCがシミュレーション結果を良好に再現していることを確認できた。

Fig. 5 Pressure dependences of the dimensionless rate constant for capillary condensation in the atomistic silica pore model mimicking MCM-41 (Pore diameter: 3.3 nm) at (a) 75, (b) 80, and (c) 87.3 K. Argon adsorption isotherms in the atomistic silica pore model calculated via the GCMC and gauge cell MC methods at (d) 75, (e) 80, and (f) 87.3 K, together with the experimental counterparts. Snapshots at the (g) multilayer adsorption state α, (h) transient state β, and (i) condensed state γ at 75 K obtained from the gauge cell MC simulation.

以上の結果により，k*_{c, GCMC}=10⁻⁴は10⁵/atom MCステップのGCMCシミュレーションにおける臨界速度定数であり，またこの値は，細孔径，細孔モデル，温度に依らない普遍的な値であることが明らかとなった。

3.2. 実測毛管凝縮圧の予測

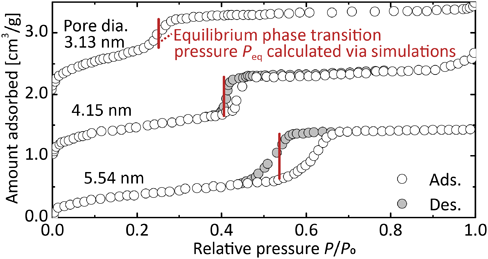
同様の手法により，実験により測定された毛管凝縮圧P_condの予測を試みた。Fig. 5d–fにMCM-41（細孔径3.3 nm）を用いて測定した75, 80, 87.3 KのAr吸着等温線を示す。また，Fig. 5 g–iにはgauge cell MCシミュレーション結果から描画した，75 Kにおける多分子層吸着状態α，遷移状態β，凝縮状態γにおけるスナップショットを示す。遷移状態βでは，液膜の厚みは多分子層吸着状態αに比べ厚くなっているものの，メニスカスの形状は円筒状を維持している。これはシリンダー型細孔内での凝縮核の形状は，ブリッジ状ではなく円筒状であることを示している。gauge cell MC法により求めた平衡転移圧P_eqは，いずれの温度においても実験の脱着枝に一致しており，毛管蒸発過程が平衡な相転移過程であることを確認できた。75 Kおよび80 Kでは毛管凝縮はP_eqよりも高圧で生じており，準安定状態からの相転移過程であることがわかる。P_eqにおいて凝縮核が生成するために必要な時間が，実験の平衡待ち時間に比べて非常に長い，つまりP_eqにおける毛管凝縮速度が非常に遅いため，P_eq<P_condとなり，ヒステリシスが観測されたと考えられる。Fig. 5dからわかるとおり，75 Kでは相対圧P_cond/P₀=0.34において毛管凝縮が進行しており，この圧力における無次元速度定数はk*(P_cond)=10⁻¹⁷であった（Fig. 5a）。この結果より，「実験の平衡待ち時間内に毛管凝縮を観測し得る十分に速い速度」を表す，実在系の臨界速度定数k*_cをk*_c=10⁻¹⁷と決定した。これを用いて80 KにおけるP_condを予測したところ（Fig. 5b），実験結果を良好に再現することに成功した（Fig. 5e）。さらに，87 KではP_eqにおいて速度定数がk*_cよりも大きいことから（Fig. 5c），P_eqにおいて毛管凝縮が進行し，吸着ヒステリシスが生じないということも予測することができた（Fig. 5f）。細孔径の異なるMCM-41（細孔径3.9 nm）においても同様に，k*_c=10⁻¹⁷を用いることで75，80，87.3 Kの毛管凝縮・吸着ヒステリシス挙動を予測可能であることも確認している。

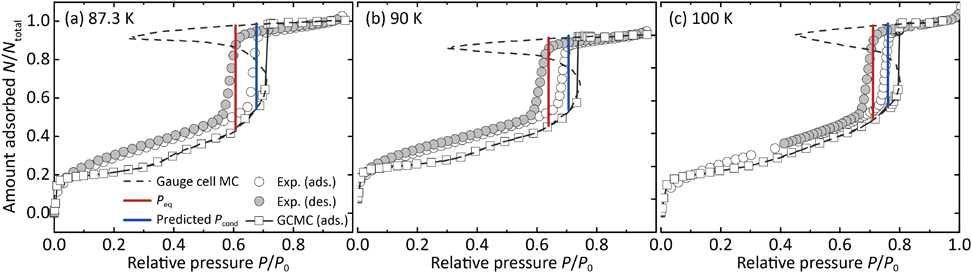
準安定状態から生じる毛管凝縮の予測手法の幅広い温度・細孔径への適用可能性を検証すべく，k*_c=10⁻¹⁷を用いてSBA-15における毛管凝縮挙動の予測を試みた。SBA-15はMCM-41同様，均一なシリンダー型細孔が規則的に配列した構造をもつ多孔性シリカ材料であり，その細孔径は通常MCM-41よりも大きい。滑らかなシリンダー型細孔によりSBA-15をモデル化し，87.3，90，100 KにおいてAr吸着等温線を計算した。滑らかなシリンダー型細孔モデルの細孔径は，87.3 Kで計算されたP_eqが実験の脱着枝に一致するよう，6.4 nmと決定した。Fig. 6に計算したAr吸着等温線を実験結果とともに示す。87.3 Kだけではなく90 Kおよび100 KにおいてもP_eqが実験の脱着枝と良好に一致していることがわかる。また，MCM-41と同様，k*_c=10⁻¹⁷を用いて実験のP_condを再現することに成功した。以上の結果から，k*_c=10⁻¹⁷は温度，細孔径に依らない普遍的な値であることが明らかとなり，この値一つで広範な温度・細孔径における毛管凝縮挙動の予測が可能となった。

Fig. 6 Argon adsorption isotherms in the smooth pore model with a pore diameter of 6.4 nm using the GCMC and gauge cell MC methods at（a）87.3,（b）90, and（c）100 K, together with the experimental adsorption isotherms for SBA-15. The estimated P_cond values were obtained using k*_c=10⁻¹⁷.

3.3. 毛管凝縮の速度定数の圧力依存性

Fig. 5a–cに示されるとおり，圧力が僅かに変化するだけで，毛管凝縮の速度定数は桁が劇的に変化していることがわかる。これは，たとえ平衡待ち時間を多少長くしたとしても，観測される毛管凝縮圧はほとんど変化しないということを意味する。このことは，サンプルが同じであれば，測定する人や場所，装置に依らず（つまり多少の測定条件の違いがあったとしても），ほぼ同じ吸着等温線が得られるという経験的な事実に符合する。また，Fig. 5aからわかるとおり，細孔径3.3 nmのMCM-41について，75 KのP_eqにおける凝縮の速度定数はk*(P_eq)=10⁻²⁷であり，これは臨界速度定数k*_c=10⁻¹⁷よりも10¹⁰分の1である。これより，この系において吸着ヒステリシスのない可逆な等温線を観測するためには，通常の10¹⁰倍の平衡待ち時間が必要であることがわかる。通常の平衡待ち時間はhourオーダー（10³ s）であるため，可逆な等温線を観測するためには，約10³ s×10¹⁰=10¹³ s=100万年の年月を待たねばならず，事実上不可能であるということが明らかとなった。

3.4. GCMC系と実在系の臨界速度定数の比較

GCMCシミュレーションにおいて，計算ステップ数を10倍（つまりは計算時間を10倍）にすると，発生確率が10分の1のレアイベントを観測できると予想される。毛管凝縮の無次元速度定数k*(μ)は毛管凝縮が発生する確率と解釈できることから，10⁵ MC step/atomではk*(μ)=k*_c,GCMC=10⁻⁴以上の確率で発生する毛管凝縮のみ観測できたことがわかる。これから，計算ステップ数を10倍の10⁶ MC step/atomとすると，k*(μ)=10⁻⁵の発生確率の毛管凝縮を観測することができる，つまり，より低圧（低化学ポテンシャル）で毛管凝縮を観測することができると予想される。したがって，GCMCシミュレーションのみで実験の毛管凝縮挙動を再現しようとするならば，実在系の臨界速度定数はk*_c=10⁻¹⁷であることから，必要な計算ステップ数は10⁵ MC/atomのk*_{c, GCMC}/k*_c=10¹³倍となる。現状，10⁵ MC/atomのシミュレーションの実施にdayオーダーの時間がかかっていることから，GCMCシミュレーションにより毛管凝縮圧を直接予測するためには，100億年オーダーの計算時間が必要であることとなり，現実的に不可能であることがわかる。

規則シリカ多孔体で観測される毛管凝縮挙動の理解・予測を目的に，遷移状態理論により毛管凝縮の速度定数を評価した。速度定数の圧力依存性に着目し，ほんの微小な圧力の変化に対して速度定数が劇的に変化していることを明らかにした。この結果は，平衡待ち時間を多少変化させたとしても観測される毛管凝縮圧はほとんど変化しないことを意味し，毛管凝縮は本質的に速度過程であるにもかかわらず，その測定の再現性が非常に高いことを保証するものである。また，GCMCシミュレーション結果と速度定数との比較により，「GCMCシミュレーション（10⁵ MC step/atom）の計算時間内に毛管凝縮を観測し得る十分に速い速度」を表す臨界速度定数がk*_{c, GCMC}=10⁻⁴であることを見出した。さらに，実在系についても同様に，実験結果と速度定数との比較により，「吸着実験の平衡待ち時間内に毛管凝縮を観測し得る十分に速い速度」である臨界速度定数がk*_c=10⁻¹⁷であることを見出した。これを決定することで，吸着ヒステリシスの発現・消失，および非平衡相転移である毛管凝縮が生じる圧力を，広範な細孔径，温度において定量的に予測することに初めて成功した。本研究により，細孔径と毛管凝縮圧が完全に対応付けられたことから，今後はこの知見に基づき，実験の毛管凝縮圧から細孔径を合理的に予測する新規手法の開発が期待される。